Question

13．在△ABC中，AB=AC，BF⊥AC于点F，CD⊥AC于点C，过点A的直线交BF、CD的延长线于点E、D，过点D作DH⊥AB于点H，求证：BE=DH．

Answer 1

分析 连结CE、BD，由垂线的性质得出BE‖CD，得出△BCD的面积=△ECD的面积，因此△ABD的面积=四边形ABCE的面积，由四边形ABCE的面积=$\frac{1}{2}$AC•BE，△ABD的面积=$\frac{1}{2}$AB•DH，AB=AC，即可得出结论．

解答 证明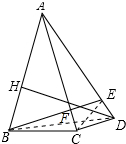：连结CE、BD，如图所示：
∵BF⊥AC，CD⊥AC，
∴BE‖CD，
∴△BCD的面积=△ECD的面积，
∴△ABD的面积=四边形ABCE的面积，
∵BF⊥AC，
∴四边形ABCE的面积=$\frac{1}{2}$AC•BE，
又∵△ABD的面积=$\frac{1}{2}$AB•DH，AB=AC，
∴BE=DH．

点评 本题考查了等腰三角形的性质、平行线的判定、三角形面积的计算等知识；证出平行线得出△BCD的面积=△ECD的面积是解决问题的关键．