题目内容
18. 如图,已知A、B两村分别距公路l的距离AA′=10km,BB′=40km,且A′B′=50km.在公路l上建一中转站P使AP+BP的值最小,则AP+BP的最小值为( )
如图,已知A、B两村分别距公路l的距离AA′=10km,BB′=40km,且A′B′=50km.在公路l上建一中转站P使AP+BP的值最小,则AP+BP的最小值为( )| A. | 100km | B. | 80km | C. | 60km | D. | 50$\sqrt{2}$km |
分析 作A关于直线A′B′的对称点C,连接BC,延长BB′,根据两点之间线段最短可知AP+BP的最小值即为BC的长,过C作BB′的垂线交直线BB′于D,根据对称的性质可求出A′C的长,由矩形的判定定理可判断出四边形A′CDB′是矩形,在Rt△BCD中由勾股定理即可求解.
解答 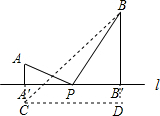 解:作A关于直线A′B′的对称点C,连接BC,延长BB′,
解:作A关于直线A′B′的对称点C,连接BC,延长BB′,
∵两点之间线段最短,
∴AP+BP的最小值即为BC的长,
过C作BB′的垂线交直线BB′于D,
∵A、C关于直线A′B′对称,AA′=10km,
∴A′C=10km,
∵AA′⊥A′B′,BB′⊥A′B′,
∴A′C∥B′D,
∵BB′⊥A′B′,CD⊥BB′,
∴A′B′∥CD,
∴四边形A′CDB′是矩形,
∴A′B′=CD=50km,BD=BB′+B′D=40+10=50km,
∴BC=$\sqrt{C{D}^{2}+B{D}^{2}}$=$\sqrt{5{0}^{2}+5{0}^{2}}$=50$\sqrt{2}$km.
故选:D.
点评 本题考查的是最短路线问题、矩形的判定定理及勾股定理,熟知两点之间线段最短是解答此题的关键.

练习册系列答案
相关题目
8.△ABC的外心在三角形的内部,则△ABC是( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 无法判断 |
9.下列命题中,属于假命题的是( )
| A. | 对顶角相等 | |
| B. | 三角形内角和等于180° | |
| C. | 全等三角形对应角相等 | |
| D. | 有三个角分别对应相等的两个三角形全等 |
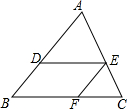 已知:如图,在△ABC中,DE∥BC,EF∥AB,$\frac{AD}{DB}$=$\frac{3}{2}$,BC=25,求:FC的长.
已知:如图,在△ABC中,DE∥BC,EF∥AB,$\frac{AD}{DB}$=$\frac{3}{2}$,BC=25,求:FC的长.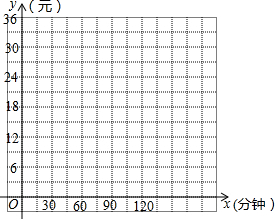 某通讯公司推出了两种移动电话收费标准:
某通讯公司推出了两种移动电话收费标准: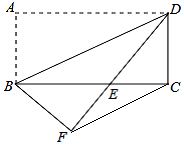 如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E.连结CF
如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E.连结CF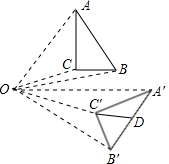 如图,Rt△ABC的斜边AB=16,Rt△ABC绕点O顺时针旋转后得到Rt△A'B'C',则Rt△A'B'C'的斜边A'B'上的中线C'D的长度为8.
如图,Rt△ABC的斜边AB=16,Rt△ABC绕点O顺时针旋转后得到Rt△A'B'C',则Rt△A'B'C'的斜边A'B'上的中线C'D的长度为8.