题目内容
设xi(i=1,2,3,…,n)为任意代数式,我们规定:y=max{x1,x2,x3,…,xn}表示x1,x2,…,xn中的最大值,如y=max{1,2}=2
(1)求y=max{x,3};
(2)借助函数图象,解决以下问题:
①解不等式 max{x+1,
}≥2
②若函数y=max{|x-1|,
x+a,x2-4x+3}的最小值为1,求实数a的值.
(1)求y=max{x,3};
(2)借助函数图象,解决以下问题:
①解不等式 max{x+1,
| 2 |
| x |
②若函数y=max{|x-1|,
| 1 |
| 2 |
考点:二次函数的性质,一次函数的性质,反比例函数的性质
专题:新定义
分析:(1)根据规定,分x≥3和x<3两种情况求解;
(2)①画出函数y=x+1和y=
的图象得到交点坐标为(1,2),然后根据规定写出不等式的解集即可;
②画出函数y=|x-1|,y=x2-4x+3的图象,可知最小值为y=
x+a与抛物线的交点,令y=1根据抛物线解析式求出x的值,再代入直线解析式求出a的值即可.
(2)①画出函数y=x+1和y=
| 2 |
| x |
②画出函数y=|x-1|,y=x2-4x+3的图象,可知最小值为y=
| 1 |
| 2 |
解答:解:(1)y=
;
(2)①

由图可知,两函数图象交点为(1,2),
∴不等式max{x+1,
}≥2的解集为x>0;
②

由图可知,最小值为y=
x+a与抛物线y=x2-4x+3的交点,
∴x2-4x+3=1,
解得x1=2-
,x2=2+
(舍去),
∴
×(2-
)+a=1,
解得a=
.
|
(2)①

由图可知,两函数图象交点为(1,2),
∴不等式max{x+1,
| 2 |
| x |
②

由图可知,最小值为y=
| 1 |
| 2 |
∴x2-4x+3=1,
解得x1=2-
| 2 |
| 2 |
∴
| 1 |
| 2 |
| 2 |
解得a=
| ||
| 2 |
点评:本题考查了二次函数的性质,一次函数的性质,反比例函数的性质,以及作函数图象,读懂题目信息,理解y=max{x1,x2,x3,…,xn}的意义是解题的关键.

练习册系列答案
相关题目
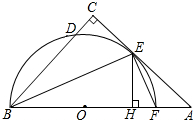 如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.
如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆. 在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P.求证:PB=PC,并直接写出图中其他相等的线段.
在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P.求证:PB=PC,并直接写出图中其他相等的线段.