Question

如图，在平面直角坐标系中，点A的坐标为（1，0），点B的坐标为（4，0），点C在y的正半轴上，且OB=2OC，在直角坐标平面内确定点D，使得以点D、A、B、C为顶点的四边形是平行四边形，请写出点D的坐标为　　．

Answer 1

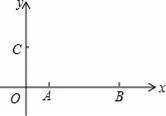
（3，2）（﹣3，2）（5，﹣2）【考点】平行四边形的判定；坐标与图形性质．

【分析】需要分类讨论：以AB为边的平行四边形和以AB为对角线的平行四边形．

【解答】解：如图，①当BC为对角线时，易求M₁（3，2）；

②当AC为对角线时，CM∥AB，且CM=AB．所以M₂（﹣3，2）；

③当AB为对角线时，AC∥BM，且AC=BM．则|M_y|=OC=2，|M_x|=OB+OA=5，所以M₃（5，﹣2）．

综上所述，符合条件的点D的坐标是M₁（3，2），M₂（﹣3，2），M₃（5，﹣2）．

故答案为：（3，2）（﹣3，2）（5，﹣2）．