题目内容
如图,AB是⊙O的直径,AD和BE是⊙O的两条切线,A,B为切点,过圆上一点C作⊙O切线CF,分别交AD、BE于点M、N,连接AC、CB、OM、ON.若AB=2,∠ABC=30°.给出以下结论:①△NBC是等边三角形;②△MON∽△ACB;③AM= ,BN=
,BN= ;④△AMC的面积与△BNC的面积之比为1:9.其中正确的结论有: (把你认为正确结论的序号都填上).
;④△AMC的面积与△BNC的面积之比为1:9.其中正确的结论有: (把你认为正确结论的序号都填上).

①②③④.
【解析】
试题分析:∵AB是⊙O直径,BE是⊙O切线,∴∠ABE=90°,∵∠ABC=30°,∴∠CBN=60°,∵CE=BE,∴△NBC是等边三角形,∴①正确;
∵△NBC是等边三角形,∴∠CNO=∠ONB=30°,∴∠EOB=60°,连接OC,∵OB=OC,且∠ABC=30°,∴∠BCO=∠ABC=30°,∵∠AOC为△BOC的外角,∴∠AOC=2∠ABC=60°,∵MA,MC分别为圆O的切线,∴MA=MC,且∠MAO=∠MCO=90°,在Rt△AOM和Rt△COM中,∵MA=MC,OM=OM,∴Rt△AOM≌Rt△COM(HL),∴∠AOM=∠COM= ∠AOC=30°,∴∠MOE=90°,在△MON和△ACB中,∵∠MON=∠ACB=90°,∠CNO=∠CBA=30°,∴△MON∽△ACB,∴②正确;
∠AOC=30°,∴∠MOE=90°,在△MON和△ACB中,∵∠MON=∠ACB=90°,∠CNO=∠CBA=30°,∴△MON∽△ACB,∴②正确;
∵在Rt△AOM中,OA= AB=1,∠AOM=30°,∴tan30°=
AB=1,∠AOM=30°,∴tan30°= ,即
,即 ,解得:AM=
,解得:AM= ,BN=
,BN= OB=
OB= ,∴③正确;
,∴③正确;
△AMC的面积= ,△BNC的面积=
,△BNC的面积= ,∴△AMC的面积与△BNC的面积之比=
,∴△AMC的面积与△BNC的面积之比= ,∴④正确.故答案为:①②③④.
,∴④正确.故答案为:①②③④.

考点:1.切线的性质;2.相似三角形的判定;3.解直角三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的系数是_______。
的系数是_______。 (
( )经过直角三角形OAB斜边OB的中点D,与直角边AB相交于点C.若△OBC的面积为3,则k=____________.
)经过直角三角形OAB斜边OB的中点D,与直角边AB相交于点C.若△OBC的面积为3,则k=____________.
 B.
B. C.
C. D.
D.

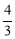 ,则t的值为 .
,则t的值为 .
 (
( )的图象如图所示,下列说法错误的是( )
)的图象如图所示,下列说法错误的是( )
 (
( 时,y随x的增大而增大;
时,y随x的增大而增大; 或
或 时,不等式
时,不等式 成立.
成立. +kx-6=0的一个根是3,则k的值是 .
+kx-6=0的一个根是3,则k的值是 .