题目内容
9.阅读材料:如果x1,x2是一元二次方程ax2+bx+c=0的两根,那么有x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.这是一元二次方程根与系数的关系,我们利用它可以用来解题,例x1,x2是方程x2+6x-3=0的两根,求x12+x22的值.解法可以这样:∵x1+x2=-6,x1x2=-3,则x12+x22=(x1+x2)2-2x1x2=(-6)2-2×(-3)=42.
请你根据以上解法解答下题:
已知x1,x2是方程x2+x-1=0的两根,求:
(1)$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$的值;
(2)(x1-x2)2的值.
(3)试求x22-x12的值.
分析 (1)由根与系数的关系可得x1+x2=-1,x1x2=-1,将其代入到$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$即可得;
(2)将x1+x2=-1,x1x2=-1代入到(x1-x2)2=(x1+x2)2-4x1x2即可得;
(3)根据x22-x12=-(x12-x22),结合(2)中结果即可得.
解答 解:(1)∵x1,x2是方程x2+x-1=0的两根,
∴x1+x2=-1,x1x2=-1,
则$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$=$\frac{-1}{-1}$=1;
(2)(x1-x2)2=(x1+x2)2-4x1x2=1+4=5;
(3)x22-x12=-(x12-x22)=-5.
点评 本题主要考查根与系数的关系,熟练掌握韦达定理是解题的关键.

练习册系列答案
相关题目
 如图,在Rt△ABC中,∠C=90°,BD是Rt△ABC的一条角平分线,点O在BD上,过O点作OE⊥BC于E,OF⊥AC于F,OE=OF.
如图,在Rt△ABC中,∠C=90°,BD是Rt△ABC的一条角平分线,点O在BD上,过O点作OE⊥BC于E,OF⊥AC于F,OE=OF.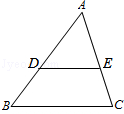 如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=6,$\frac{AD}{BD}$=$\frac{3}{4}$,求CE的长.
如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=6,$\frac{AD}{BD}$=$\frac{3}{4}$,求CE的长.