题目内容
8.计算:(1)在Rt△ABC中,∠C=90°,a=8,b=15,求c;
(2)在Rt△ABC中,∠C=90°,a=3,b=4,求c.
分析 (1)直接利用勾股定理进行解答即可;
(2)直接利用勾股定理进行解答即可.
解答 解:(1)利用勾股定理,得c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{{8}^{2}+1{5}^{2}}$=17,即c=17;
(2)利用勾股定理,得c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,即c=5.
点评 本题考查了勾股定理.在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.
如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.

练习册系列答案
相关题目
19.有两根长度分别为15cm和25cm的小木棒,在下列长度的小木棒中选取一根,使之能与已有的两根搭成一个直角三角形,那么应该选取( )
| A. | 40cm | B. | 30cm | C. | 20cm | D. | 17cm |
16.某生姜种植基地计划种植A、B两种生姜30亩,已知A、B两种生姜的年产量分别为2000千克/亩、2500千克/亩.若该基地收获A、B两种生姜的年总产量为68000千克,求A、B两种生姜各种多少亩?
3.汽车油箱中的余油量Q(升)随汽车行驶的时间t(时)的变化而变化,Q与t之间的关系为Q=a-5t,其中a是油箱中原有的油的升数,若这辆汽车油箱中原有油60升.
(1)用表格表示行驶1到5小时过程中这辆汽车油箱中余油量与行驶时间t的关系,填写下表:
(2)这辆车最多可行驶多少小时?
(1)用表格表示行驶1到5小时过程中这辆汽车油箱中余油量与行驶时间t的关系,填写下表:
| 行驶时间(时) | 1 | 2 | 3 | 4 | 5 |
| 余油量(升) | 55 | 50 | 45 | 40 | 35 |
17.下列长度的三条线段能组成钝角三角形的是( )
| A. | 3,4,4 | B. | 3,4,5 | C. | 3,4,7 | D. | 3,4,6 |
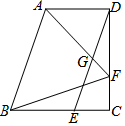 如图,在四边形ABCD中,AD∥BC,∠C=90°,BC=CD,点E,F分别在边BC,CD上,
如图,在四边形ABCD中,AD∥BC,∠C=90°,BC=CD,点E,F分别在边BC,CD上,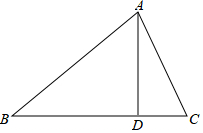 如图,D为△ABC边BC上的一点,AB=20,AC=13,AD=12,DC=5,则S△ABC=126.
如图,D为△ABC边BC上的一点,AB=20,AC=13,AD=12,DC=5,则S△ABC=126.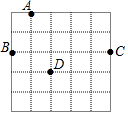 如图,在5×5的正方形网格中,从在格点上的点A,B,C,D中任取三点,所构成的三角形恰好是直角三角形的个数为( )
如图,在5×5的正方形网格中,从在格点上的点A,B,C,D中任取三点,所构成的三角形恰好是直角三角形的个数为( )