题目内容
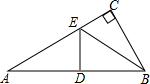 如图,在△ABC中,∠C=90°,点E时AC上一点,ED⊥AB于D,cosA=
如图,在△ABC中,∠C=90°,点E时AC上一点,ED⊥AB于D,cosA=| 2 |
| 5 |
| 5 |
| 4 |
| 3 |
| 5 |
考点:解直角三角形
专题:计算题
分析:在直角三角形AED与直角三角形BED中,利用锐角三角函数定义表示出cosA与tan∠BED,设AD=2x,则有AE=
x,利用勾股定理表示出ED,进而表示出DB,得到AB与AC,在直角三角形ABC中,利用锐角三角函数定义表示出cosA,列出关于x的方程,求出方程的解即可得到DE的长.
| 5 |
解答:解:在Rt△AED和Rt△BED中,
cosA=
=
,tan∠BED=
=
,
设AD=2x,则有AE=
x,
根据勾股定理得:ED=x,BD=
x,
∴AB=AD+DB=2x+
x=
x,AC=AE+EC=
x+
,
在Rt△ABC中,cosA=
=
,
即
=
,
解得:x=3,
则DE=3.
cosA=
| AD |
| AE |
2
| ||
| 5 |
| BD |
| ED |
| 4 |
| 3 |
设AD=2x,则有AE=
| 5 |
根据勾股定理得:ED=x,BD=
| 4 |
| 3 |
∴AB=AD+DB=2x+
| 4 |
| 3 |
| 10 |
| 3 |
| 5 |
| 5 |
在Rt△ABC中,cosA=
| AC |
| AB |
2
| ||
| 5 |
即
| ||||
|
2
| ||
| 5 |
解得:x=3,
则DE=3.
点评:此题考查了解直角三角形,涉及的知识有:锐角三角函数定义,勾股定理,熟练掌握锐角三角函数定义是解本题的关键.

练习册系列答案
相关题目
侧面展开图是一个长方形的几何体是( )
| A、圆锥 | B、圆柱 | C、棱锥 | D、球 |
 如图,⊙O是△ABC的外接圆,连接OA、OB,∠AOB=80°,则∠C的度数为( )
如图,⊙O是△ABC的外接圆,连接OA、OB,∠AOB=80°,则∠C的度数为( )| A、30° | B、40° |
| C、50° | D、80° |
 在△ABC和△ADE中,AC=AB,AE=AD,∠CAB=∠EAD=90°.
在△ABC和△ADE中,AC=AB,AE=AD,∠CAB=∠EAD=90°. 因为一次函数y=kx+b与y=-kx+b(k≠0)的图象关于y轴对称,所以我们定义:函数y=kx+b与y=-kx+b(k≠0)互为“镜子”函数.
因为一次函数y=kx+b与y=-kx+b(k≠0)的图象关于y轴对称,所以我们定义:函数y=kx+b与y=-kx+b(k≠0)互为“镜子”函数.