题目内容
已知如图，一张矩形报纸ABCD的长AB=acm，宽BC=bcm，E、F分别为AB、CD的中点．若矩形AEFD与矩形ABCD相似，则a：b等于（ ）A、
| ||
B、1：
| ||
C、
| ||
D、1：
|
考点：相似多边形的性质
专题：
分析：根据线段中点的定义表示出AE，再根据相似多边形的对应边成比例列式计算即可得解．
解答：解：∵E、F分别为AB、CD的中点，
∴AE=
AB=
cm，
∵矩形AEFD与矩形ABCD相似，
∴
=
，
即
=
，
整理得，a2=2b2，
解得a=
b，
所以，a：b=
：1．
故选A．
∴AE=
| 1 |
| 2 |
| a |
| 2 |
∵矩形AEFD与矩形ABCD相似，
∴
| AD |
| AB |
| AE |
| AD |
即
| b |
| a |
| ||
| b |
整理得，a2=2b2，
解得a=
| 2 |
所以，a：b=
| 2 |
故选A．
点评：本题考查了相似多边形的性质，主要利用了相似多边形的对应边成比例，熟记性质是解题的关键．
练习册系列答案
相关题目
甲、乙两人在相同的条件下，各射靶10次，经过计算：甲、乙的平均数均是7，甲的方差是1.2，乙的方差是1.8，则下列说法中不正确的是（ ）
| A、甲、乙射中的总环数相同 |
| B、甲的成绩稳定 |
| C、乙的成绩波动较大 |
| D、甲、乙的众数相同 |
用同样大小的黑色棋子按如图所示的规律摆放，那么2013个图形的黑色棋子有（ ）
| A、6041个 |
| B、6042个 |
| C、6142个 |
| D、6143个 |
二次根式
中字母的取值范围是（ ）
| 2-x |
| A、x≥2 | B、x＜2 |
| C、x＞2 | D、x≤2 |
如图的几何体是由4个相同的小正方体组成．其左视图为（ ）A、 |
B、 |
C、 |
D、 |
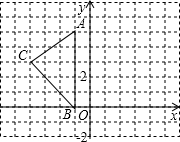如图，在平面直角坐标系中，已知A（-1，5），B（-1，0），C（-4，3）．
如图，AD∥BC，∠A=∠C，BE、DF分别平分∠ABC和∠CDA．求证：BE∥DF．