Question

【题目】已知等腰中，，的顶点在线段上，不与重合.

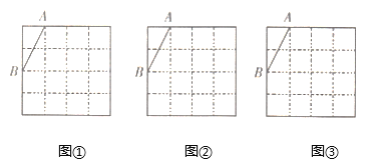
（1）如图①，若且点在中点时，四边形是什么四边形并证明？

（2）将绕点旋转至如图②所示位置，若，设的面积为；的面积为，求的值（用含有的代数式表示）.

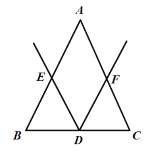
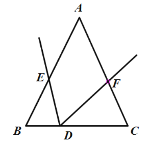
图① 图②

Answer 1

【答案】（1）菱形；（2）.

【解析】

（1）根据菱形的判定方法进行证明即可；

（2）首先证明△EBD∽△DCF，设BE=x，CF=y，可得xy=mn，由S1=mxsinα，S2=nysinα，可得S1S2=（mn）2sin2α;

（1）菱形，

∵点D为BC的中点，且

∴为三角形中位线，

∴

∵

∴DE=DF

∵,

∴AEDF是平行四边形，

∴AEDF是菱形.

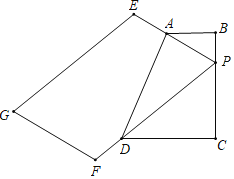
（2）设BE=x，CF=y．

∵∠EDC=∠EDF+∠FDC=∠B+∠BEF，∠MDN=∠B，

∴∠BED=∠FDC，

∵∠B=∠C，

∴△BED∽△CDF，

∴，

∴，

∴

∵S1=BDBEsinα=mxsinα，S2=CDCFsinα=ysinα，

∴