Question

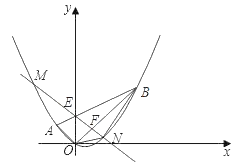
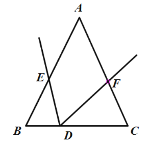
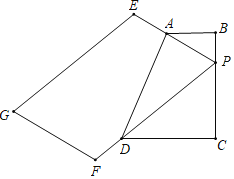
【题目】在四边形ABCD中，AB∥CD，BC⊥CD，AB＝2，CD＝3，在BC上取点P（P与B、C不重合）连接PA延长至E，使PA＝2AE，连接PD并延长至F，使PD＝3FD，以PE、PF为边作平行四边形，另一个顶点为G，则PG长度的最小值为_____．

Answer 1

【答案】7

【解析】

作如下辅助线：连接PG、EF交于点O，PG交AD于点K，过点A作AM∥EO交PG于点M，过点D作DN∥FO交PG于点N，由此可得△POE∽△PMA，△POF∽△PND，△AKM∽△DKN，利用对应边成比例即可求出平行四边形的对角线PG必过点K，且 ，当KP⊥BC时，PG的长度最小，此时PK＝，所以OP＝，PG＝2OP＝7．

解：连接PG、EF交于点O，PG交AD于点K，过点A作AM∥EO交PG于点M，过点D作DN∥FO交PG于点N．

∵PA＝2AE，PD＝3FD，

∴，．

∵AM∥EO，DN∥FO，

∴△POE∽△PMA，△POF∽△PND，

∴，

，

∴MP＝OP，NP＝OP，AM＝EO，DN＝FO，

又∵在平行四边形PEGF中，OE＝OF，

∴，

∵AM∥DN，

∴，

∵，

∴，

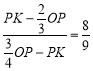解得：OP＝PK．

由题意可知，PG必过点K，当KP⊥BC时，PG最小，此时PK＝ ，

∴OP＝PK＝，

∴PG＝2OP＝7．

故答案为：7．