Question

4．如图，正方形ABCD的边长为a，E为边CD上一动点，连结AE交对角线BD于点P，过点P作PF⊥AE交BC于点F．
（1）求证：PA=PF．
小明给出了以下证明思路：过点P作PM⊥AB于点N，只要证△PAM≌△PFN即可得证．请你帮小明完成证明过程．
（2）过点F作FQ⊥BD于点Q，在点E的运动过程中，PQ的长度是否发生变化？若不变，求出PQ的长；若变化，请说明变化规律．
（3）请你写出线段AB，BF，BP之间满足的数量关系，不必说明理由．

Answer 1

分析 （1）连结PC，由正方形的性质得到AB=BC，∠ABP=∠CBP，然后依据SAS证明△APB≌△CPB，由全等三角形的性质可知PA=PC，∠PCB=∠PAB，接下来利用四边形的内角和为360°可证明∠PFC=∠PCF，于是得到PF=PC，故此可证明PF=PA．
（2）连结AC交BD于点O，依据正方形的性质可知△AOB为等腰直角三角形，于是可求得AO的长，接下来，证明△APO≌△PFQ，依据全等三角形的性质可得到PQ=AO；
（3）过点P作PM⊥AB，PN⊥BC，垂足分别为M，N，首先证明△PBN为等腰直角三角形于是得到PN+BN=$\sqrt{2}$PB，由角平分线的性质可得到PM=PN，然后再依据LH证明△PAM≌△PFN可得到FN=AM，PM=PN，于是将AB+BF=可转化为BN+PN的长．

解答 解：（1）证明：连结PC．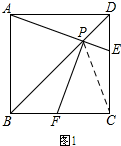

∵ABCD为正方形，
∴AB=BC，∠ABP=∠CBP．
在△APB和△CPB中$\left\{\begin{array}{l}{AB=BC}\\{∠ABP=∠CBP}\\{BP=BP}\end{array}\right.$，
∴△APB≌△CPB．
∴PA=PC，∠PCB=∠PAB．
∵∠ABF=∠APF=90°，
∴∠PAB+∠PFB=180°．
∵∠PFC+∠PFB=180°，
∴∠PFC=∠PAB．
∴∠PFC=∠PCF．
∴PF=PC．
∴PF=PA．
（2）PQ的长不变．
理由：连结AC交BD于点O，如图2．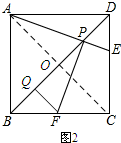

∵PF⊥AE，
∴∠APO+∠FPQ=90°．
∵FQ⊥BD，
∴∠PFQ+∠FPQ=90°．
∴∠APO=∠PFQ．
又∵四边形ABCD为正方形，
∴∠AOP=∠PQF=90°，AO=$\frac{\sqrt{2}}{2}$a．
在△APO和△PFQ中，$\left\{\begin{array}{l}{∠AOP=∠PQF=90°}\\{∠APO=∠PFQ}\\{AP=PF}\end{array}\right.$，
∴△APO≌△PFQ．
∴PQ=AO=$\frac{\sqrt{2}}{2}$a．
（3）如图3所示：过点P作PM⊥AB，PN⊥BC，垂足分别为M，N．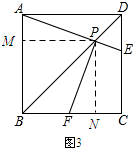

∵四边形ABCD为正方形，
∴∠PBN=45°．
∵PN⊥BN，
∴BN=PN=$\frac{\sqrt{2}}{2}$BP．
∴BN+PN=$\sqrt{2}$PB．
∵BD平分∠ABC，PM⊥AB，PN⊥BC，
∴PM=PN．
在△PAM和△PFN中，$\left\{\begin{array}{l}{PA=PF}\\{PM=PN}\end{array}\right.$，
∴△PAM≌△PFN．
∴AM=FN．
∵∠MBN=∠BNP=∠BMP=90°，
∴MB=PN．
∴AB+BF=AM+MB+BF=FN+BF+PN=BN+PN=$\sqrt{2}$PB．

点评 本题主要考查的是四边形的综合应用，解答本题主要应用了全等三角形的性质和判断、正方形的性质、角平分线的性质、特殊锐角三角函数值、矩形的判断，掌握本题的辅助线的作法是解题的关键．