题目内容
15.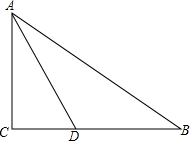 如图:在△ABC中,∠C=90°,AD平分∠CAB交BC于点D,sinB=$\frac{3}{5}$,AB=10,求D到AB的距离.
如图:在△ABC中,∠C=90°,AD平分∠CAB交BC于点D,sinB=$\frac{3}{5}$,AB=10,求D到AB的距离.
分析 过点D作DE⊥AB于E,根据角平分线上的点到角的两边距离相等可得DE=CD,然后解直角三角形求出AC,再利用勾股定理列式求出BC,然后利用△ABC的面积列出方程求解即可.
解答 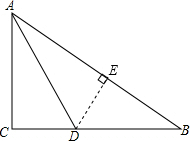 解:如图,过点D作DE⊥AB于E,
解:如图,过点D作DE⊥AB于E,
∵∠C=90°,AD平分∠CAB,
∴DE=CD,
∵sinB=$\frac{3}{5}$,AB=10,
∴AC=10×$\frac{3}{5}$=6,
由勾股定理得,BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{{10}^{2}-{6}^{2}}$=8,
△ABC的面积=$\frac{1}{2}$AC•CD+$\frac{1}{2}$AB•DE=$\frac{1}{2}$AC•BC,
即$\frac{1}{2}$×6•DE+$\frac{1}{2}$×10•DE=$\frac{1}{2}$×6×8,
解得DE=3,
即D到AB的距离3.
点评 本题考查了角平分线上的点到角的两边距离相等的性质,三角形的面积,熟记性质并利用三角形的面积列出方程是解题的关键.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
5.若分式$\frac{1}{x+5}$有意义,则x的取值范围是( )
| A. | x≠5 | B. | x≠-5 | C. | x>5 | D. | x>-5 |
20.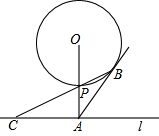 如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.若在⊙O上存在点Q,使△QAC是以AC为底边的等腰三角形,则⊙O的半径的最小值为( )
如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.若在⊙O上存在点Q,使△QAC是以AC为底边的等腰三角形,则⊙O的半径的最小值为( )
 如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.若在⊙O上存在点Q,使△QAC是以AC为底边的等腰三角形,则⊙O的半径的最小值为( )
如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.若在⊙O上存在点Q,使△QAC是以AC为底边的等腰三角形,则⊙O的半径的最小值为( )| A. | $\frac{5}{2}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $\frac{5\sqrt{3}}{3}$ |
7.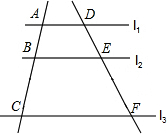 如图,如果l1∥l2∥l3,则下列各式不正确的是( )
如图,如果l1∥l2∥l3,则下列各式不正确的是( )
 如图,如果l1∥l2∥l3,则下列各式不正确的是( )
如图,如果l1∥l2∥l3,则下列各式不正确的是( )| A. | $\frac{BC}{AC}$=$\frac{EF}{DF}$ | B. | $\frac{AB}{BC}$=$\frac{EF}{DE}$ | C. | $\frac{AB}{DE}$=$\frac{AC}{DF}$ | D. | $\frac{AB}{AC}$=$\frac{DE}{DF}$ |
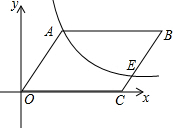 如图,平行四边形OABC中,OC=6,点P(4,8)在直线OA上,点E在BC上,BE=2CE,反比例函数y=$\frac{k}{x}$的图象经过A、E的两点,则k=$\frac{81}{8}$.
如图,平行四边形OABC中,OC=6,点P(4,8)在直线OA上,点E在BC上,BE=2CE,反比例函数y=$\frac{k}{x}$的图象经过A、E的两点,则k=$\frac{81}{8}$.