Question

矩形ABCD一条边AD=8，将矩形ABCD折叠，使得点B落在CD边上的点P处．

（1）如图1，已知折痕与边BC交于点O，连接AP、OP、OA．

①求证：△OCP∽△PDA；

②若△OCP与△PDA的面积比为1：4，求边AB的长．

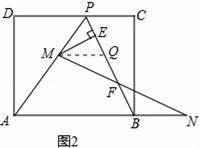
（2）如图2，在（1）的条件下，擦去AO和OP，连接BP．动点M在线段AP上（不与点P、A重合），动点N在线段AB的延长线上，且BN=PM，连接MN交PB于点F，作ME⊥BP于点E．试问动点M、N在移动的过程中，线段EF的长度是否发生变化？若不变，求出线段EF的长度；若变化，说明理由．

　

Answer 1

【考点】相似形综合题．

【分析】（1）①先证出∠C=∠D=90°，再根据∠1+∠3=90°，∠1+∠2=90°，得出∠2=∠3，即可证出△OCP∽△PDA；

②根据△OCP与△PDA的面积比为1：4，得出CP=AD=4，设OP=x，则CO=8﹣x，由勾股定理得 x²=（8﹣x）²+4²，求出x，最后根据AB=2OP即可求出边AB的长；

（2）作MQ∥AN，交PB于点Q，求出MP=MQ，BN=QM，得出MP=MQ，根据ME⊥PQ，得出EQ=PQ，根据∠QMF=∠BNF，证出△MFQ≌△NFB，得出QF=QB，

再求出EF=PB，由（1）中的结论求出PB==4，最后代入EF=PB即可得出线段EF的长度不变．

【解答】解：（1）①如图1，∵四边形ABCD是矩形，

∴∠C=∠D=90°，

∴∠1+∠3=90°，

∵由折叠可得∠APO=∠B=90°，

∴∠1+∠2=90°，

∴∠2=∠3，

又∵∠D=∠C，

∴△OCP∽△PDA；

②如图1，∵△OCP与△PDA的面积比为1：4，

∴===，

∴CP=AD=4，

设OP=x，则CO=8﹣x，

在Rt△PCO中，∠C=90°，

由勾股定理得 x²=（8﹣x）²+4²，

解得：x=5，

∴AB=AP=2OP=10，

∴边AB的长为10；

（2）作MQ∥AN，交PB于点Q，如图2，

∵AP=AB，MQ∥AN，

∴∠APB=∠ABP=∠MQP．

∴MP=MQ，

∵BN=PM，

∴BN=QM．

∵MP=MQ，ME⊥PQ，

∴EQ=PQ．

∵MQ∥AN，

∴∠QMF=∠BNF，

在△MFQ和△NFB中，

，

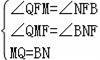
∴△MFQ≌△NFB（AAS）．

∴QF=QB，

∴EF=EQ+QF=PQ+QB=PB，

由（1）中的结论可得：PC=4，BC=8，∠C=90°，

∴PB==4，

∴EF=PB=2，

∴在（1）的条件下，当点M、N在移动过程中，线段EF的长度不变，它的长度为2．

【点评】此题考查了相似形综合，用到的知识点是相似三角形的判定与性质、全等三角形的判定与性质、勾股定理、等腰三角形的性质，关键是做出辅助线，找出全等和相似的三角形．