Question

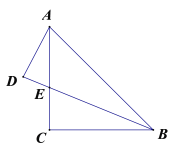
【题目】如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D，E为BC上一点，连接AE，作EF⊥AE交AB于F．

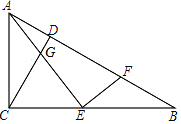
（1）求证：△AGC∽△EFB．

（2）除（1）中相似三角形，图中还有其它相似三角形吗？如果有，请把它们都写出来．

Answer 1

【答案】（1）详见解析；（2）详见解析.

【解析】

（1）由CD⊥AB，EF⊥AE，得到∠FDG=∠FEG=90°，求出∠BFE=∠DGE，根据相似三角形的判定得到结论即可；

（2）根据相似三角形的判定解答即可．

（1）证明：∵CD⊥AB，EF⊥AE

∴∠FDG=∠FEG=90°

∴∠DGE+∠DFE=360°﹣90°﹣90°=180°

又∠BFE+∠DFE=180°，

∴∠BFE=∠DGE，

又∠DGE=∠AGC

∴∠AGC=∠BFE，

又∠ACB=∠FEG=90°

∴∠AEC+∠BEF=180°﹣90°=90°，∠AEC+∠EAC=90°，

∴∠EAC=∠BEF，

∴△AGC∽△EFB

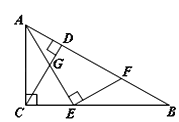
（2）解：有．

∵∠GAD=∠FAE，∠ADG=∠AEF=90°，

∴△AGD∽△AFE；

∴∠CAD=∠BAC，

∴△ACD∽△ABC，

同理得△BCD∽△BAC，

∴△ACD∽△CBD，

即△ACD∽△ABC∽△CBD，