Question

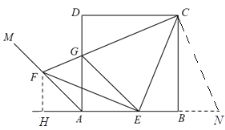
【题目】如图，正方形ABCD的边长为a，射线AM是∠A外角的平分线，点E在边AB上运动(不与点A、B重合)，点F在射线AM上，且AF=√2BE，CF与AD相交于点G，连结EC、EF、EG．

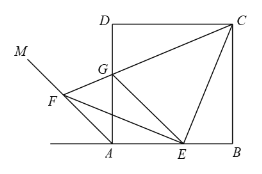
（1）求证：CE=EF；

（2）求△AEG的周长(用含a的代数式表示)

（3）试探索：点E在边AB上运动至什么位置时，△EAF的面积最大?

Answer 1

【答案】（1）见解析；（2）2a；（3）点在边中点时，最大，最大值为

【解析】

（1）过点作于点，依据SAS证明，即可求证；

（2）先在（1）的基础上继续证明是等腰直角三角；把绕点逆时针旋转至位置，即可证明（SAS），从而得到，继而得到△AEG的周长；

（3）设，由（1）得，建立二次函数，即可求出最值.

（1）证明：如图，过点作于点，则

平分，

是等腰直角三角形，

，，

，

又

（2）

又在中，

由（1）知，

是等腰三角形，

把绕点逆时针旋转至位置，如图所示．

，，

，

又

（SAS）

（3）设，由（1）得

则

当，即点在边中点时，最大，最大值为．