题目内容

20．如图，把一张长方形纸片沿EF折叠后，点C，点D分别落在点N，点M的位置，若∠EFB=50°，则∠BGM等于（　　）
A．50°B．60°C．70°D．80°

分析 首先求出∠FEG的度数，根据∠EGF=180°-∠FEG-∠EFG，求出∠EGF即可解决问题．

解答 解：∵AD∥BC，
∴∠DEF=∠EFG=∠FEG=50°，
∴∠EGF=180°-∠FEG-∠EFG=80°，
∴∠BGM=∠EGF=80°，
故选D．

点评 本题考查平行线的性质，对顶角相等、翻折变换等知识，解题的关键是熟练应用平行线的性质，利用翻折不变性解决问题，属于中考常考题型．

练习册系列答案
相关题目
10．阅读理解，解决问题：
同学们玩游戏，借助两个三角形模板画平行线．
规则1：摆放一副三角板，画平行线．
小颖是这样做的：如图1，先画一条直线MN，之后摆放三角板，得到AB∥CD．依据是同位角相等，两直线平行．
小静如图2摆放三角板，也得到AB∥CD．依据是内错角相等，两直线平行．
规则2：请你利用图3中所示的两个三角形模板摆放后画平行线．在图4中画出你摆放的两个三角形模板的位置．
11．若关于x的方程$\frac{2}{x-1}$+$\frac{mx}{{x}^{2}-1}$=0有增根，则m的值为（　　）
A．1B．0C．-4D．0或-4
8．4的平方根是（　　）
A．±2B．$\frac{1}{2}$C．2D．-2
15．若点A（-$\frac{1}{2}$，-$\frac{1}{a}$）在第三象限的角平分线上，则a的值为（　　）
A．$\frac{1}{2}$B．-$\frac{1}{2}$C．2D．-2
5．下列运算正确的是（　　）
A．2m•m3=2m6B．（3m）2=6m2C．（m+4）2=m2+16D．（-1）0+（-1）3=0
12．已知4x6ya÷32xby-2=$\frac{1}{8}$x2y3，那么（　　）
A．a=2，b=3B．a=1，b=4C．a=3，b=6D．a=4，b=5
9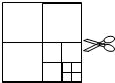．如图，将一张正方形纸片剪成四个小正方形，得到4个小正方形，称为第一次操作；然后，将其中的一个正方形再剪成四个小正方形，共得到7个小正方形，称为第二次操作；再将其中的一个正方形再剪成四个小正方形，共得到10个小正方形，称为第三次操作；…，根据以上操作，若要得到2017个小正方形，则需要操作的次数是（　　）
A．672B．671C．670D．674
10．下列运算中，正确的是（　　）
A．x3÷x=x4B．a2+a2=2a4C．3x-2x=1D．3x-2x=x

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网