题目内容
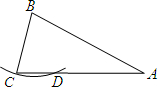 如图,在△ABC中,AB=AC=2BC,以点B为圆心,BC长为半径作弧,与AC交于点D.若AC=4,则线段CD的长为( )
如图,在△ABC中,AB=AC=2BC,以点B为圆心,BC长为半径作弧,与AC交于点D.若AC=4,则线段CD的长为( )A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
考点:相似三角形的判定与性质
专题:压轴题
分析:首先连接BD,易证得△ABC∽△BDC,然后由相似三角形的对应边成比例,求得线段CD的长.
解答: 解:连接BD,
解:连接BD,
∵AB=AC,BC=BD,
∴∠ABC=∠C,∠C=∠BDC,
∴∠ABC=∠BDC,
∴△ABC∽△BDC,
∴
=
,
∵在△ABC中,AB=AC=2BC,AC=4,
∴BC=2,
∴CD=
=1.
故选B.
 解:连接BD,
解:连接BD,∵AB=AC,BC=BD,
∴∠ABC=∠C,∠C=∠BDC,
∴∠ABC=∠BDC,
∴△ABC∽△BDC,
∴
| AC |
| BC |
| BC |
| CD |
∵在△ABC中,AB=AC=2BC,AC=4,
∴BC=2,
∴CD=
| BC2 |
| AC |
故选B.
点评:此题考查了相似三角形的判定与性质以及等腰三角形的性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
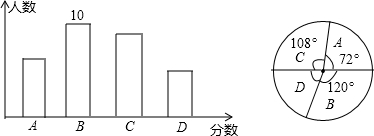 某校组织学生绘画比赛,对参赛作品按A、B、C、D四个等级进行评定:四个等级的分数分别为A级5分,B级4分,C级2分,D级1分.现随机抽取部分学生绘画作品的评定结果进行分析,并绘制如下条形图和扇形统计图,根据图中信息,这些学生的平均分数是( )
某校组织学生绘画比赛,对参赛作品按A、B、C、D四个等级进行评定:四个等级的分数分别为A级5分,B级4分,C级2分,D级1分.现随机抽取部分学生绘画作品的评定结果进行分析,并绘制如下条形图和扇形统计图,根据图中信息,这些学生的平均分数是( )| A、3.0 | B、3.1 |
| C、3.2 | D、3.3 |
下列命题:
①如果一个角的两边分别垂直于另一个角的两边,那么这两个角相等;
②三角形的内心到三角形各顶点的距离都相等;
③相等的圆心角所对的弧相等;
④等弦所对的圆周角相等.
其中正确结论的个数有( )
①如果一个角的两边分别垂直于另一个角的两边,那么这两个角相等;
②三角形的内心到三角形各顶点的距离都相等;
③相等的圆心角所对的弧相等;
④等弦所对的圆周角相等.
其中正确结论的个数有( )
| A、0个 | B、1个 | C、2个 | D、3个 |
-
的倒数是( )
| 2 |
| 5 |
A、-
| ||
B、
| ||
C、
| ||
D、|-
|
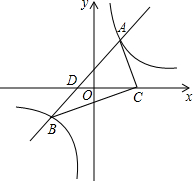 如图,在平面直角坐标系中,直线y=kx+b(k≠0)分别交双曲线
如图,在平面直角坐标系中,直线y=kx+b(k≠0)分别交双曲线
 如图,某数学活动小组为了测量我市文化广场的标志建筑“太阳鸟”的高度AB,在D处用高1.2米的测角仪CD,测得最高点A的仰角为32.6°,再向“太阳鸟”的方向前进20米至D′处,测得最高点A的仰角为45°,点D、D′、B在同一条直线上.求“太阳鸟”的高度AB.(精确到0.1米)
如图,某数学活动小组为了测量我市文化广场的标志建筑“太阳鸟”的高度AB,在D处用高1.2米的测角仪CD,测得最高点A的仰角为32.6°,再向“太阳鸟”的方向前进20米至D′处,测得最高点A的仰角为45°,点D、D′、B在同一条直线上.求“太阳鸟”的高度AB.(精确到0.1米)