题目内容
4.(1)|-3|+(-1)2011×(π-3)0-$\root{3}{27}$(2)|1-$\sqrt{2}$|-$\frac{1}{2}$$\sqrt{24}$-$\frac{2}{\sqrt{2}}$
(3)解方程组$\left\{\begin{array}{l}{7x+3y-36=0}\\{2x+9y-51=0}\end{array}\right.$
(4)解方程组$\left\{\begin{array}{l}{\frac{x}{3}-\frac{y}{4}=1}\\{3x-4y=2}\end{array}\right.$.
分析 (1)原式利用乘方的意义,零指数幂法则,平方根、立方根定义计算即可得到结果;
(2)原式利用绝对值的代数意义,二次根式性质计算即可得到结果;
(3)方程组整理后,利用加减消元法求出解即可;
(4)方程组整理后,利用加减消元法求出解即可.
解答 解:(1)原式=3-1-3=-1;
(2)原式=$\sqrt{2}$-1-$\sqrt{6}$-$\sqrt{2}$=-1-$\sqrt{6}$;
(3)方程组整理得:$\left\{\begin{array}{l}{7x+3y=36①}\\{2x+9y=51②}\end{array}\right.$,
①×3-②得:19x=57,即x=3,
把x=3代入①得:y=5,
则方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=5}\end{array}\right.$;
(4)方程组整理得:$\left\{\begin{array}{l}{4x-3y=12①}\\{3x-4y=2②}\end{array}\right.$,
①×4-②×3得:7x=42,即x=6,
把x=6代入①得:y=4,
则方程组的解为$\left\{\begin{array}{l}{x=6}\\{y=4}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
5.一件衣服提高价格25%后发现销路不是很好,欲恢复原价,则应降价( )
| A. | 40% | B. | 20% | C. | 25% | D. | 15% |
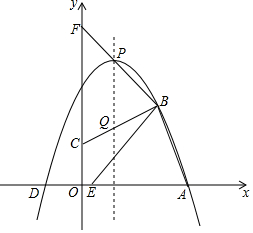 如图,二次函数y=ax2+bxc的图象经过A(4,0),D(-1,0)和B(3,3)三,.顶点为点P.作BC⊥BA交y轴于C,交对称轴于Q,将∠CBA绕点B顺时针旋转,∠CBA的两边分别交x轴、y轴于点E、F.设点E的坐标为(m,0).
如图,二次函数y=ax2+bxc的图象经过A(4,0),D(-1,0)和B(3,3)三,.顶点为点P.作BC⊥BA交y轴于C,交对称轴于Q,将∠CBA绕点B顺时针旋转,∠CBA的两边分别交x轴、y轴于点E、F.设点E的坐标为(m,0).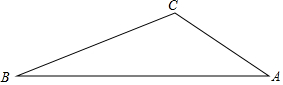 如图,在△ABC中,∠B=30°,AC=2$\sqrt{3}$,BC=6,求sinA的值.
如图,在△ABC中,∠B=30°,AC=2$\sqrt{3}$,BC=6,求sinA的值.