题目内容
13．若实数a，b满足|3a-1|+（b-2）2=0，则ab的值为$\frac{2}{3}$．分析 根据非负数的性质列方程求出a、b的值，然后相乘计算即可得解．
解答 解：由题意得，3a-1=0，b-2=0，
解得a=$\frac{1}{3}$，b=2，
所以，ab=$\frac{1}{3}$×2=$\frac{2}{3}$．
故答案为：$\frac{2}{3}$．
点评 本题考查了非负数的性质：几个非负数的和为0时，这几个非负数都为0．
练习册系列答案
相关题目
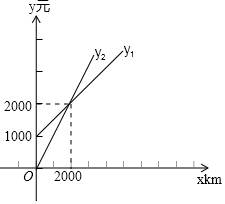某单位需要用车，准备和一个体车主或一国有出租公司其中的一家签订合同，设汽车每月行驶x km，应付给个体车主的月租费是y1元，付给出租车公司的月租费是y2元，y1，y2分别与x之间的函数关系图象是如图所示的两条直线，观察图象，回答下列问题：
如图，正方形ABCD中，P是BD上的一个动点，E在BC上，且BE=2，CE=1，则PE+PC的最小值为$\sqrt{13}$．