题目内容
(1)如图1,O是△ABC内一点,且BO,CO分别平分∠ABC,∠ACB、若∠A=46°,则∠BOC=(2)如图2,O是△ABC外一点,BO,CO分别平分△ABC的外角∠CBE,∠BCF.若∠A=n°,求∠BOC;
(3)如图3,O是△ABC外一点,BO,CO分别平分∠ABC,∠ACD.若∠A=n°,求∠BOC.
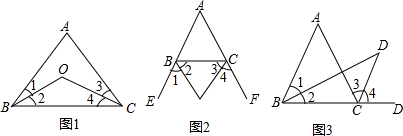
分析:(1)在△BOC中,把∠COB根据三角形的内角和用∠OBC和∠OCB表示,然后利用BO,CO分别平分∠ABC,∠ACB和三角形的内角和即可用∠A表示∠BOC;
(2)和(1)一样,把∠COB根据三角形的内角和用∠OBC和∠OCB表示,然后利用BO,CO分别平分∠ABC,∠ACB和三角形外角和内角关系就可以用∠A表示∠BOC;
(3)首先在△BOC中,根据三角形的外角和内角的关系得到∠COB=∠4-∠2,同理∠A=∠ACD-∠ABC,后利用BO,CO分别平分∠ABC,∠ACB即可得到∠A和∠BOC的关系;
(2)和(1)一样,把∠COB根据三角形的内角和用∠OBC和∠OCB表示,然后利用BO,CO分别平分∠ABC,∠ACB和三角形外角和内角关系就可以用∠A表示∠BOC;
(3)首先在△BOC中,根据三角形的外角和内角的关系得到∠COB=∠4-∠2,同理∠A=∠ACD-∠ABC,后利用BO,CO分别平分∠ABC,∠ACB即可得到∠A和∠BOC的关系;
解答:解:(1)∵∠COB=180°-(∠OBC+∠OCB),
而BO,CO分别平分∠ABC,∠ACB,
∴∠OBC=
∠ABC,∠OCB=
∠ACB
∴∠BOC=180°-
(∠ABC+∠ACB)
=180°-
(180°-∠A)
=90°+
∠A
=113°,
故∠BOC=113°.
∴若∠A=n°,则∠BOC=90°+
n°;
(2)∵∠COB=180°-(∠OBC+∠OCB),
而BO,CO分别平分∠ABC,∠ACB,
∴∠OBC=
∠EBC,∠OCB=
∠FCB
∴∠BOC=180°-
(∠EBC+∠FCB),
而∠EBC=180°-∠ABC,∠FCB=∠180°-∠ACB
∴∠BOC=180°-
(180°+∠A)
=90°-
∠A,
∴∠BOC=90°-
n°;
(3)∵∠COB=∠4-∠2,∠A=∠ACD-∠ABC,
而BO,CO分别平分∠ABC,∠ACD,
∴∠ACD=2∠4,∠ABC=2∠2,
∴∠A=2∠COB,
∴∠BOC=
n°.
而BO,CO分别平分∠ABC,∠ACB,
∴∠OBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOC=180°-
| 1 |
| 2 |
=180°-
| 1 |
| 2 |
=90°+
| 1 |
| 2 |
=113°,
故∠BOC=113°.
∴若∠A=n°,则∠BOC=90°+
| 1 |
| 2 |
(2)∵∠COB=180°-(∠OBC+∠OCB),
而BO,CO分别平分∠ABC,∠ACB,
∴∠OBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOC=180°-
| 1 |
| 2 |
而∠EBC=180°-∠ABC,∠FCB=∠180°-∠ACB
∴∠BOC=180°-
| 1 |
| 2 |
=90°-
| 1 |
| 2 |
∴∠BOC=90°-
| 1 |
| 2 |
(3)∵∠COB=∠4-∠2,∠A=∠ACD-∠ABC,
而BO,CO分别平分∠ABC,∠ACD,
∴∠ACD=2∠4,∠ABC=2∠2,
∴∠A=2∠COB,
∴∠BOC=
| 1 |
| 2 |
点评:本题是一道开放性题目,考查了同学们利用角平分线的性质、三角形的内角、外角等知识理解决问题的能力,有利于培养同学们的发散思维能力.

练习册系列答案
相关题目
 如图,点C是⊙O优弧ACB上的中点,弦AB=6cm,E为OC上任意一点,动点F从点A出发,以每秒1cm的速度沿AB方向向点B匀速运动,若y=AE2-EF2,则y与动点F的运动时间x(0≤x≤6)秒的函数关系式为
如图,点C是⊙O优弧ACB上的中点,弦AB=6cm,E为OC上任意一点,动点F从点A出发,以每秒1cm的速度沿AB方向向点B匀速运动,若y=AE2-EF2,则y与动点F的运动时间x(0≤x≤6)秒的函数关系式为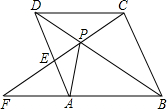 如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD于E,交BA的延长线于点F.
如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD于E,交BA的延长线于点F. 反比例函数y=
反比例函数y= 11、如图,点D是△ABC的边BC延长线上的一点,∠A=70°,∠ACD=105°,则∠B=
11、如图,点D是△ABC的边BC延长线上的一点,∠A=70°,∠ACD=105°,则∠B= 如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.
如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.