题目内容
 已知:如图,△ABC,射线AM平分∠BAC.
已知:如图,△ABC,射线AM平分∠BAC.(1)尺规作图(不写作法,保留作图痕迹)作BC的中垂线,与AM相交于点G,连接BG、CG.
(2)在(1)的条件下,∠BAC和∠BGC的等量关系为
考点:作图—基本作图,线段垂直平分线的性质
专题:
分析:(1)以C、B为圆心,大于
BC为半径作弧,两弧交于F、E,作直线FE即为BC的垂直平分线.
(2)作MD⊥AB,MK⊥AC,利用角平分线的性质和垂直平分线的性质证全等即可.
| 1 |
| 2 |
(2)作MD⊥AB,MK⊥AC,利用角平分线的性质和垂直平分线的性质证全等即可.
解答:
 解:(1)如图1:
解:(1)如图1:
(2)互补.
证明:作MD⊥AB,MK⊥AC,
∵AM为∠BAC的平分线,
∴MD=MK,
∵EF为BC的垂直平分线,
∴MB=MC,
在△MBD与△MCK中,
,
∴△MBD≌△MCK(HL),
∴∠BMC=∠DMK,
∵∠DMK+∠BAC=180°,
∴∠BMC+∠BAC=180°,
∴∠BAC和∠BGC互补.
故答案为:互补.

 解:(1)如图1:
解:(1)如图1:(2)互补.
证明:作MD⊥AB,MK⊥AC,
∵AM为∠BAC的平分线,
∴MD=MK,
∵EF为BC的垂直平分线,
∴MB=MC,
在△MBD与△MCK中,
|
∴△MBD≌△MCK(HL),
∴∠BMC=∠DMK,
∵∠DMK+∠BAC=180°,
∴∠BMC+∠BAC=180°,
∴∠BAC和∠BGC互补.
故答案为:互补.
点评:本题考查了作图--基本作图,要熟悉垂直平分线的性质和角平分线的性质.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
-
的倒数是( )
| 1 |
| 2 |
A、
| ||
| B、2 | ||
| C、-2 | ||
D、-
|
某学校要开展游园互动,计划买一批铅笔和橡皮擦,铅笔每支0.6元,橡皮擦每块0.8元,用300元钱买了铅笔和橡皮擦共365份,其中买了铅笔多少支?若设买了铅笔x支,则下列方程正确的是( )
| A、0.6x+0.8x=300 | ||||
B、
| ||||
| C、0.6x+0.8(300-x)=365 | ||||
D、
|
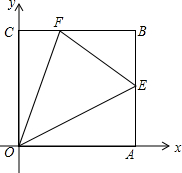 如图,正方形OABC中点B(4,4),点E、F分别在AB、BC上,∠EOF=45°.
如图,正方形OABC中点B(4,4),点E、F分别在AB、BC上,∠EOF=45°.  如图,AD是△ABC的中线,DE⊥AB于点E,DF⊥AC于F,且BE=CF,问AD是否平分∠BAC,如果是,请说明理由.
如图,AD是△ABC的中线,DE⊥AB于点E,DF⊥AC于F,且BE=CF,问AD是否平分∠BAC,如果是,请说明理由.