题目内容
直线y=
x+
与x轴，y轴分别相交于A，B两点，圆心P的坐标为（1，0），圆P与y轴相切于点O．若将圆P沿x轴向左移动，当圆P与该直线第一次相切时，点P的横坐标为（ ）
A．-1
B．-2
C．-3
D．-4
【答案】分析：由题意可知，OA=3，OB=
，得到∠BAO的度数为30°．当圆P与该直线第一次相切时，设切点是点D，连接PD，则PD=1，在Rt△ADP中AP=2PD=2，故有OP=OA-AP=1．
解答：
解：⊙P与该直线第一次相切时，设切点是点D，连接PD，则PD=1，
由题意知OA=3，OB=
，
∴根据∠A的正切值就可得到∠BAO的度数为30°，
∴在Rt△ADP中，AP=2PD=2，
OP=OA-AP=3-2=1，
∴点P的横坐标为-1．
故选A．
点评：本题应注意直线与圆相切时，圆心到直线的距离应等于圆的半径．
，得到∠BAO的度数为30°．当圆P与该直线第一次相切时，设切点是点D，连接PD，则PD=1，在Rt△ADP中AP=2PD=2，故有OP=OA-AP=1．解答：
解：⊙P与该直线第一次相切时，设切点是点D，连接PD，则PD=1，由题意知OA=3，OB=
，∴根据∠A的正切值就可得到∠BAO的度数为30°，
∴在Rt△ADP中，AP=2PD=2，
OP=OA-AP=3-2=1，
∴点P的横坐标为-1．
故选A．
点评：本题应注意直线与圆相切时，圆心到直线的距离应等于圆的半径．
练习册系列答案
黄冈创优卷系列答案
相关题目
21、如图，在平面直角坐标系中，已知点A坐标为（2，4），直线x=2与x轴相交于点B，连接OA，抛物线y=x2从点O沿OA方向平移，与直线x=2交于点P，顶点M到A点时停止移动．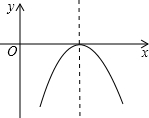
轴相交于C，D两点．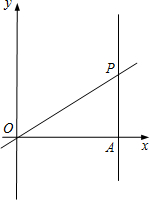
点O、直线AP绕着点A以相同的速度逆时针方向旋转，旋转过程中，两条直线交点始终为P，当直线OP与y轴正半轴重合时，两条直线同时停止转动．
如图，在平面直角坐标系内，直线AB分别与x轴、y轴交于B、A两点，且OB=2OA，S△ABO=16．