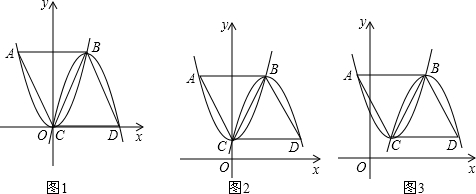
题目内容
(2012•衢州二模)如图,平面直角坐标系中,直线y=
x与直线x=3交于点P,点A是直线x=3与x轴的交点,将直线OP绕着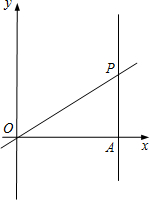 点O、直线AP绕着点A以相同的速度逆时针方向旋转,旋转过程中,两条直线交点始终为P,当直线OP与y轴正半轴重合时,两条直线同时停止转动.
点O、直线AP绕着点A以相同的速度逆时针方向旋转,旋转过程中,两条直线交点始终为P,当直线OP与y轴正半轴重合时,两条直线同时停止转动.
(1)当旋转角度为15°时,点P坐标为
(2)整个旋转过程中,点P所经过的路线长为
π
π.
| ||
| 3 |
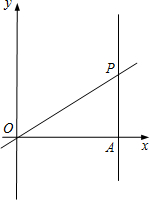 点O、直线AP绕着点A以相同的速度逆时针方向旋转,旋转过程中,两条直线交点始终为P,当直线OP与y轴正半轴重合时,两条直线同时停止转动.
点O、直线AP绕着点A以相同的速度逆时针方向旋转,旋转过程中,两条直线交点始终为P,当直线OP与y轴正半轴重合时,两条直线同时停止转动.(1)当旋转角度为15°时,点P坐标为
(
,
)
3+
| ||
| 2 |
3+
| ||
| 2 |
(
,
)
;3+
| ||
| 2 |
3+
| ||
| 2 |
(2)整个旋转过程中,点P所经过的路线长为
2
| ||
| 3 |
2
| ||
| 3 |
分析:(1)首先根据题意可求得旋转前点P的坐标,即可得OA的长,当旋转角度为15°时,过点P作PC⊥OA于C,作AB⊥OP于B,由∠POA=30°+15°=45°,∠OAP=90°-15°=75°,利用解直角三角形的知识可求得点P的坐标;
(2)可得整个旋转过程中,点P所经过的路线是圆弧.根据题意作出图形,然后设P2是
的中点,D是圆心,连接P2D并延长,交P1P3于点C,交OA于E,连接P2A,P2O,P1D,利用垂径定理,可求得半径的长,由特殊角的三角函数值,求得圆心角的度数,然后利用弧长公式求解即可求得答案.
(2)可得整个旋转过程中,点P所经过的路线是圆弧.根据题意作出图形,然后设P2是
 |
| P1P3 |
解答:解:∵直线y=
x与直线x=3交于点P,
∴点P的坐标为:(3,
),
∴OA=3,
∴tan∠POA=
=
,
∴∠POA=30°.
 (1)如图,当旋转角度为15°时,
(1)如图,当旋转角度为15°时,
过点P作PC⊥OA于C,作AB⊥OP于B,
∵∠POA=30°+15°=45°,∠OAP=90°-15°=75°,
∴∠BAO=∠POA=45°,
∴∠BAP=∠OAP-∠BAO=75°-45°=30°,
在Rt△OAB中,OB=AB=OA•cos∠POA=3×
=
,
在Rt△ABP中,BP=AB•tan∠PAB=
×
=
,
∴OP=OB+BP=
+
,
在Rt△OCP中,OC=PC=OP•sin∠POA=(
+
)×
=
,
∴点P的坐标为:(
,
);
(2)整个旋转过程中,点P所经过的路线是圆弧.
当两条直线停止转动时,点P到点P3处,如图2,
则∠AOP3=90°,
∴OP旋转了60°,
∴∠OAP3=90°-60°=30°,
∴OP3=OA•tan∠OAP=3×
=
;
∴P1P3∥OA,
则点P所经过的路线如图3,
设P2是
的中点,D是圆心,
连接P2D并延长,交P1P3于点C,交OA于E,连接P2A,P2O,P1D,
∴P2C⊥P1P3,P2C⊥OA,P1C=P3C=OE=AE=
AC=
,
∴P2A=P2O,
∴∠P2OA=∠P2AO,
设旋转角为x°,
则∠P2AO=90°-x°,∠P2OA=30°+x°,
∴90-x=30+x,
解得:x=30,
∴∠P2OA=60°,
∴P2E=OE•tan∠P2OA=
×
=
,
∴P2C=P2E-CE=
,
设半径为r,
则r2=(
)2+(r-
)2,
解得:r=
,
∴CD=r-P2C=
,
∴tan∠CP3D=
=
,
∴∠CP3D=∠CP1D=30°,
∴∠P1DP3=120°,
∴整个旋转过程中,点P所经过的路线长为:
=
π.
故答案为:(1)(
,
);(2)
π.
| ||
| 3 |
∴点P的坐标为:(3,
| 3 |
∴OA=3,
∴tan∠POA=
| PA |
| OA |
| ||
| 3 |
∴∠POA=30°.
 (1)如图,当旋转角度为15°时,
(1)如图,当旋转角度为15°时,过点P作PC⊥OA于C,作AB⊥OP于B,
∵∠POA=30°+15°=45°,∠OAP=90°-15°=75°,
∴∠BAO=∠POA=45°,
∴∠BAP=∠OAP-∠BAO=75°-45°=30°,
在Rt△OAB中,OB=AB=OA•cos∠POA=3×
| ||
| 2 |
3
| ||
| 2 |
在Rt△ABP中,BP=AB•tan∠PAB=
3
| ||
| 2 |
| ||
| 3 |
| ||
| 2 |
∴OP=OB+BP=
3
| ||
| 2 |
| ||
| 2 |
在Rt△OCP中,OC=PC=OP•sin∠POA=(
3
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
3+
| ||
| 2 |
∴点P的坐标为:(
3+
| ||
| 2 |
3+
| ||
| 2 |
(2)整个旋转过程中,点P所经过的路线是圆弧.
当两条直线停止转动时,点P到点P3处,如图2,
则∠AOP3=90°,
∴OP旋转了60°,
∴∠OAP3=90°-60°=30°,
∴OP3=OA•tan∠OAP=3×
| ||
| 3 |
| 3 |

∴P1P3∥OA,
则点P所经过的路线如图3,
设P2是
 |
| P1P3 |
连接P2D并延长,交P1P3于点C,交OA于E,连接P2A,P2O,P1D,
∴P2C⊥P1P3,P2C⊥OA,P1C=P3C=OE=AE=
| 1 |
| 2 |
| 3 |
| 2 |
∴P2A=P2O,
∴∠P2OA=∠P2AO,
设旋转角为x°,
则∠P2AO=90°-x°,∠P2OA=30°+x°,
∴90-x=30+x,
解得:x=30,
∴∠P2OA=60°,
∴P2E=OE•tan∠P2OA=
| 3 |
| 2 |
| 3 |
3
| ||
| 2 |
∴P2C=P2E-CE=
| ||
| 2 |
设半径为r,
则r2=(
| 3 |
| 2 |
| ||
| 2 |
解得:r=
| 3 |
∴CD=r-P2C=
| ||
| 2 |
∴tan∠CP3D=
| CD |
| P3C |
| ||
| 3 |
∴∠CP3D=∠CP1D=30°,
∴∠P1DP3=120°,
∴整个旋转过程中,点P所经过的路线长为:
120×π×
| ||
| 180 |
2
| ||
| 3 |
故答案为:(1)(
3+
| ||
| 2 |
3+
| ||
| 2 |
2
| ||
| 3 |
点评:此题考查了一次函数的交点问题、解直角三角形的知识、特殊角的三角函数值、垂径定理以及弧长公式等知识.此题综合性较强,难度较大,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
 (2012•衢州二模)如图是某区“平改坡”工程中一种坡屋顶的设计图.已知原平屋顶的宽度AB为8米,两条相等的斜面钢条AC、BC夹角为110°,过点C作CD⊥AB于D.
(2012•衢州二模)如图是某区“平改坡”工程中一种坡屋顶的设计图.已知原平屋顶的宽度AB为8米,两条相等的斜面钢条AC、BC夹角为110°,过点C作CD⊥AB于D. 、乙两班离A地的距离分别为y1千米、y2千米,y1、y2与x的函数关系图象如图所示,根据图象解答下列问题:
、乙两班离A地的距离分别为y1千米、y2千米,y1、y2与x的函数关系图象如图所示,根据图象解答下列问题: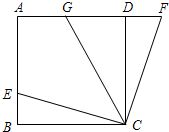 (2012•衢州二模)如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE=
(2012•衢州二模)如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE=