题目内容
 如图,E、F是正方形ABCD的边AD上的两个动点,满足AE=DF.连接CF交BD于G,连接BE交AG于H.已知正方形ABCD的边长为4cm,解决下列问题:
如图,E、F是正方形ABCD的边AD上的两个动点,满足AE=DF.连接CF交BD于G,连接BE交AG于H.已知正方形ABCD的边长为4cm,解决下列问题:(1)求证:BE⊥AG;
(2)求线段DH的长度的最小值.
考点:正方形的性质,全等三角形的判定与性质
专题:
分析:(1)根据正方形的性质可得AB=AD=CD,∠BAD=∠CDA,∠ADG=∠CDG,然后利用“边角边”证明△ABE和△DCF全等,根据全等三角形对应角相等可得∠1=∠2,利用“边角边”证明△ADG和△CDG全等,根据全等三角形对应角相等可得∠2=∠3,从而得到∠1=∠3,然后求出∠AHB=90°,再根据垂直的定义证明即可;
(2)根据直角三角形斜边上的中线等于斜边的一半,取AB的中点O,连接OH、OD,然后求出OH=
AB=1,利用勾股定理列式求出OD,然后根据三角形的三边关系可知当O、D、H三点共线时,DH的长度最小.
(2)根据直角三角形斜边上的中线等于斜边的一半,取AB的中点O,连接OH、OD,然后求出OH=
| 1 |
| 2 |
解答:(1)证明:在正方形ABCD中,AB=AD=CD,∠BAD=∠CDA,∠ADG=∠CDG,
在△ABE和△DCF中,
,
∴△ABE≌△DCF(SAS),
∴∠1=∠2,
在△ADG和△CDG中,
,
∴△ADG≌△CDG(SAS),
∴∠2=∠3,
∴∠1=∠3,
∵∠BAH+∠3=∠BAD=90°,
∴∠1+∠BAH=90°,
∴∠AHB=180°-90°=90°,
∴BE⊥AG;
(2)解:如图,取AB的中点O,连接OH、OD,
则OH=AO=
AB=2,
在Rt△AOD中,OD=
=
=2
,
根据三角形的三边关系,OH+DH>OD,
∴当O、D、H三点共线时,DH的长度最小,
DH的最小值=OD-OH=2
-2.
在△ABE和△DCF中,
|
∴△ABE≌△DCF(SAS),
∴∠1=∠2,
在△ADG和△CDG中,
|
∴△ADG≌△CDG(SAS),

∴∠2=∠3,
∴∠1=∠3,
∵∠BAH+∠3=∠BAD=90°,
∴∠1+∠BAH=90°,
∴∠AHB=180°-90°=90°,
∴BE⊥AG;
(2)解:如图,取AB的中点O,连接OH、OD,
则OH=AO=
| 1 |
| 2 |
在Rt△AOD中,OD=
| OA2+AD2 |
| 22+42 |
| 5 |
根据三角形的三边关系,OH+DH>OD,
∴当O、D、H三点共线时,DH的长度最小,
DH的最小值=OD-OH=2
| 5 |
点评:本题考查了正方形的性质,全等三角形的判定与性质,直角三角形斜边上的中线等于斜边的一半的性质,三角形的三边关系,确定出DH最小时点H的位置是解题关键,也是本题的难点.

练习册系列答案
相关题目
 如图,矩形ABCD中,AB=5cm,BC=10cm,动点M从点D出发,按折线DCBAD方向以3cm/s的速度运动,动点N从点D出发,按折线DABCD方向以2cm/s的速度运动.点E在线段BC上,且BE=1cm,若M、N两点同时从点D出发,到第一次相遇时停止运动.
如图,矩形ABCD中,AB=5cm,BC=10cm,动点M从点D出发,按折线DCBAD方向以3cm/s的速度运动,动点N从点D出发,按折线DABCD方向以2cm/s的速度运动.点E在线段BC上,且BE=1cm,若M、N两点同时从点D出发,到第一次相遇时停止运动. 如图,△ACD、△ABE、△BCF均为△ABC的边BC所在直线同侧的等边三角形.
如图,△ACD、△ABE、△BCF均为△ABC的边BC所在直线同侧的等边三角形.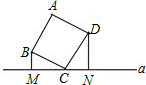 如图,正方形ABCD的顶点C在直线a上,且点B,D到a的距离分别是1,2.则这个正方形的边长是
如图,正方形ABCD的顶点C在直线a上,且点B,D到a的距离分别是1,2.则这个正方形的边长是