题目内容
17.在平面直角坐标系内,已知点A(5,3),如果点A关于直线y=kx+3的对称点落在x轴上,则k的值是-$\frac{1}{3}$或-3.分析 求得直线l:y=kx+3与y轴的交点D的坐标(0,3),根据轴对称的性质得出DP=DA=5,然后根据勾股定理即可求得对称点P的坐标,进而求得PA的中点坐标,代入直线解析式即可求得k的值.
解答 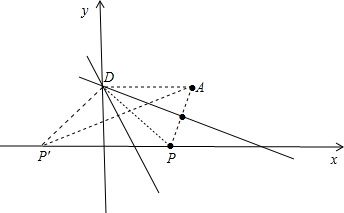 解:∵直线y=kx+3交y轴于D(0,3),A(5,3),
解:∵直线y=kx+3交y轴于D(0,3),A(5,3),
设A点关于直线y=kx+3的对称点为P(a,0),则DP=DA=5,
∵OD=3,
∴OP=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴P(4,0)或(-4,0),
∴AP的中点坐标为($\frac{9}{2}$,$\frac{3}{2}$)或($\frac{1}{2}$,$\frac{3}{2}$),
分别代入y=kx+3求得k=-$\frac{1}{3}$或-3.
故答案为-$\frac{1}{3}$或-3.
点评 本题考查了轴对称的性质,勾股定理的应用,待定系数法,求得DP=DA=5是解题的关键.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
9.下列方程中,是一元二次方程的是( )
| A. | 3x2+4 | B. | x2+y=3 | C. | x2-4=0 | D. | x2+$\frac{1}{2x}$+4=0 |
 在平面直角坐标系xOy中,直线y=-2x+1与y轴交于点C,直线y=x+k(k≠0)与y轴交于点A,与直线y=-2x+1交于点B,设点B的横坐标为x0.
在平面直角坐标系xOy中,直线y=-2x+1与y轴交于点C,直线y=x+k(k≠0)与y轴交于点A,与直线y=-2x+1交于点B,设点B的横坐标为x0.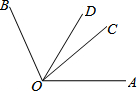 如图,已知∠COB=2∠AOC,OD平分∠AOB,且∠COD=23°,求∠AOB的度数.
如图,已知∠COB=2∠AOC,OD平分∠AOB,且∠COD=23°,求∠AOB的度数. 已知:如图△ABC中,AB=AC,∠C=30°,AB⊥AD,AD=5cm,求BC的长.
已知:如图△ABC中,AB=AC,∠C=30°,AB⊥AD,AD=5cm,求BC的长.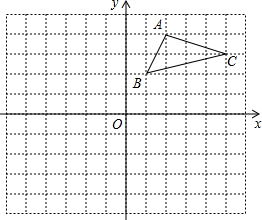 如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:
如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题: