题目内容
20. 如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F点处,已知CE=6cm,AB=16cm,求BF的长.
如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上F点处,已知CE=6cm,AB=16cm,求BF的长.
分析 由矩形ABCD,得到四个角为直角,对边相等,再由折叠的性质及勾股定理即可求出BF的长.
解答 解:∵矩形ABCD,
∴∠B=∠C=∠D=90°,AB=CD,AD=BC,
由折叠可得∠AFE=∠D=90°,AF=AD=AB,DE=EF,
∵CE=6cm,AB=DC=16cm,
∴EF=DE=DC-CE=10cm,
在Rt△EFC中,根据勾股定理得:FC=$\sqrt{1{0}^{2}-{6}^{2}}$=8cm,
设AD=BC=AF=x,则有BF=BC-FC=(x-8)cm,
在Rt△ABF中,根据勾股定理得:162+(x-8)2=x2,
解得:x=20,即x-8=20-8=12,
则BF=12cm.
点评 此题考查了翻折变换,矩形的性质,勾股定理,熟练掌握翻折的性质是解本题的关键.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
10.为了了解某社区居民的用电情况,随机对该社区10户居民进行了调查,下表是这10户居民2014年4月份用电量的调查结果:
下列结论不正确的是( )
| 居民户数 | 1 | 3 | 2 | 4 |
| 月用电量(度/户) | 40 | 50 | 55 | 60 |
| A. | 众数是60 | B. | 平均数是54 | C. | 中位数是55 | D. | 方差是29 |
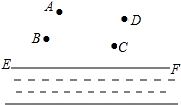 如图,在A、B、C、D四个村庄,为备战春耕,政府准备修建一个蓄水池.
如图,在A、B、C、D四个村庄,为备战春耕,政府准备修建一个蓄水池.