题目内容
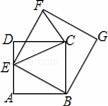
如图,点E为正方形ABCD中AD边上的动点,AB=2,以BE为边画正方形BEFG,连结CF和CE,则△CEF面积的最小值为 .


 .
.
【考点】正方形的性质.
【分析】过点F作FM⊥AD延长线于点M,令EF与CD的交点为N点,设AE=x.根据三角形的面积公式可知S△CEF=
 CN•ME,由此可知当CN最小时△CEF的面积取最小值.根据给定的条件已经角的计算找出“∠AEB=∠MFE,∠ABE=∠MEF”,从而证出△ABE≌△MEF,即得出MF=AE,ME=AB,再通过相似三角形的性质用含x的关系式表示出DN的长度,根据二项式的性质即可找出DN的最大值,将其代入前面的面积公式中即可得出结论.
CN•ME,由此可知当CN最小时△CEF的面积取最小值.根据给定的条件已经角的计算找出“∠AEB=∠MFE,∠ABE=∠MEF”,从而证出△ABE≌△MEF,即得出MF=AE,ME=AB,再通过相似三角形的性质用含x的关系式表示出DN的长度,根据二项式的性质即可找出DN的最大值,将其代入前面的面积公式中即可得出结论.
【解答】解:过点F作FM⊥AD延长线于点M,令EF与CD的交点为N点,如图所示.


则S△CEF=
 CN•ME.
CN•ME.
∵四边形ABCD为正方形,四边形BEFG为正方形,
∴∠A=90°,∠BEF=90°,BE=EF,
∴∠AEB+∠ABE=90°,∠MEF+∠MFE=90°,∠AEB+∠BEF+∠MEF=180°,
∴∠AEB=∠MFE,∠ABE=∠MEF.
在△ABE和△MEF中,

 ,
,
∴△ABE≌△MEF(ASA).
∴MF=AE,ME=AB.
∵CD⊥AD,FM⊥AD,
∴ND∥FM,
∴△EDN∽△AMF,
∴
 .
.
设AE=x,则ED=AD﹣AE=2﹣x,EM=AB=2,MF=AE=x,
∴DN=
 =﹣x2+x=﹣
=﹣x2+x=﹣
 (x﹣1)2+
(x﹣1)2+
 ≤
≤
 .
.
∴CN=CD﹣DN≥2﹣
 ≥
≥
 .
.
∴△CEF面积的最小值为
 CN•ME=
CN•ME=
 ×
×
 ×2=
×2=
 .
.
故答案为:
 .
.
【点评】本题考查了正方形的性质、全等三角形的判定及性质、相似三角形的判定及性质、三角形的面积公式及二次函数的性质,解题的关键是找出线段DN的最大值.本题属于中档题,难度不大,解决该题型题目时,根据三角形的面积公式找出其去最值的条件,再结合二次函数的性质去解决最值问题.

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案为了掌握某次数学模拟考试卷的命题质量与难度系数,命题教师选取一个水平相当的初三年级进行调研,命题教师将随机抽取的部分学生成绩(得分为整数,满分为150分)分为5组:第一组75~90;第二组90~105;第三组105~120;第四组120~135;第五组135~150.统计后得到如图所示的频数分布直方图(每组含最小值不含最大值)和扇形统计图.观察图形的信息,回答下列问题:
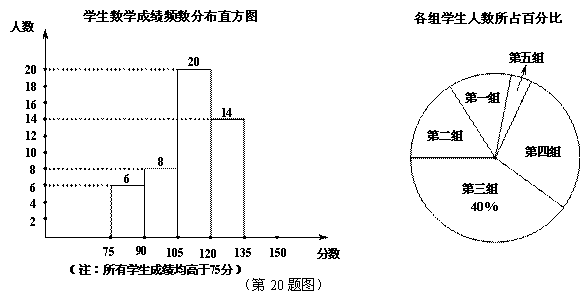 |
请将频数分布直方图补充完整;若老师找到第五组中一个学生的语文、数学、英语三科成绩,如下表.老师将语文、数学、英语成绩按照3:5:2的比例给出这位同学的综合分数.求此同学的综合分数.
| 科目 | 语文 | 数学 | 英语 |
| 得分 | 120 | 146 | 140 |
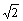 米,坡角(即∠BAC)为 45º, BC⊥ AC.现计划在斜坡中点 D 处挖去部分斜坡,修建一个平行于水平线 AC 的休闲平台 DE 和一条新的斜坡 BE ,若修建的斜坡 BE 的坡比为
米,坡角(即∠BAC)为 45º, BC⊥ AC.现计划在斜坡中点 D 处挖去部分斜坡,修建一个平行于水平线 AC 的休闲平台 DE 和一条新的斜坡 BE ,若修建的斜坡 BE 的坡比为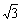 :1 ,求休闲平台 DE 的长是多少米?(结果保留根号).
:1 ,求休闲平台 DE 的长是多少米?(结果保留根号).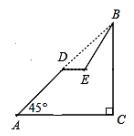

 ,则BC的长为 .
,则BC的长为 .



 有意义的条件是 .
有意义的条件是 .

 B.
B. C.
C. D.
D.