题目内容
13. 如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点.
如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点.(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标.
分析 (1)由题意抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点,利用待定系数法求出b,c的值,得出函数解析式即可;
(2)利用配方法化为顶点式求得对称轴与顶点坐标即可.
解答 解:(1)∵抛物线y=x2+bx+c与x轴的两个交点分别为A(-1,0),B(3,0),
∴$\left\{\begin{array}{l}{1-b+c=0}\\{9+3b+c=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=-2}\\{c=-3}\end{array}\right.$.
∴所求抛物线的解析式为:y=x2-2x-3;
(2)∵y=x2-2x-3=(x-1)2-4,
∴该抛物线的对称轴为直线x=1,顶点坐标为(1,-4).
点评 此题考查抛物线与x轴的交点坐标,待定系数法求函数的解析式,掌握待定系数法求函数解析式的步骤与方法是解决问题的关键.

练习册系列答案
相关题目
8.已知线段a=2,b=8,线段c是线段a、b的比例中项,则c=( )
| A. | 2 | B. | ±4 | C. | 4 | D. | 8 |
5.下列运算正确的是( )
| A. | ab2+a2b=2a2b2 | B. | -3ab+ab=-4ab | C. | a2-a=a | D. | m2n-nm2=0 |

 如图,在△ABC的外部作等腰三角形ACE和等腰三角形ABD,使AB=AD,AC=AE,∠DAB=∠CAE=45°,连接BE,CD.
如图,在△ABC的外部作等腰三角形ACE和等腰三角形ABD,使AB=AD,AC=AE,∠DAB=∠CAE=45°,连接BE,CD. 如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0)、(-3,1),AB=AC.
如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0)、(-3,1),AB=AC.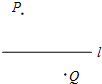 已知:如图,点P,点Q分别代表两个小区,直线l代表两个小区中间的一条公路.根据居民出行的需要,计划在公路l上的某处设置一个公交站点.
已知:如图,点P,点Q分别代表两个小区,直线l代表两个小区中间的一条公路.根据居民出行的需要,计划在公路l上的某处设置一个公交站点.