题目内容
如图,在⊙O中,点P在直径AB的延长线上,PC,PD与⊙O相切,切点分别为点C,点D,连接CD交AB于点E.如果⊙O的半径等于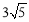 ,tan∠CPO=
,tan∠CPO=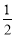 ,求弦CD的长.
,求弦CD的长.

12.
【解析】
试题分析:连接OC.由 PC和PD是⊙O的切线,得到 OC⊥PC ,PC=PD,∠OPC=∠OPD,而 CD⊥OP,CD=2CE,由tan∠CPO= ,得到tan∠OCE=tan∠CPO=
,得到tan∠OCE=tan∠CPO= ,设 OE=k,则CE=2k,OC=
,设 OE=k,则CE=2k,OC= .由⊙O的半径等于
.由⊙O的半径等于 ,得到k的值,从而得到CD的值.
,得到k的值,从而得到CD的值.
试题解析:【解析】
连接OC.∵ PC,PD与⊙O相切,切点分别为点C,点D,∴ OC⊥PC ,PC=PD,∠OPC=∠OPD,∴ CD⊥OP,CD=2CE,∵tan∠CPO= ,∴tan∠OCE=tan∠CPO=
,∴tan∠OCE=tan∠CPO= ,设 OE=k,则CE=2k,OC=
,设 OE=k,则CE=2k,OC= .(
.( )∵ ⊙
)∵ ⊙ 的半径等于
的半径等于 ,∴
,∴  ,解得
,解得 ,∴ CE=6,∴ CD=2CE=12 .
,∴ CE=6,∴ CD=2CE=12 .

考点:1.切线的性质;2.解直角三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 与直线
与直线 的交点坐标为(4,3),则方程组
的交点坐标为(4,3),则方程组 的解为 .
的解为 .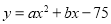 .其图象如图.
.其图象如图.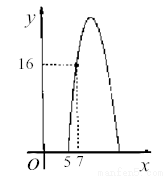
 B.
B. C.
C. D.
D.

 °.
°.
 B.
B. C.
C. D.
D.
 的图象向右平移2个单位,再向下平移3个单位,得到的抛物线是( )
的图象向右平移2个单位,再向下平移3个单位,得到的抛物线是( ) B.
B.
 D.
D.

