题目内容
如图,在⊙O中,AB,CD是直径,BE是切线,B为切点,连接AD,BC,BD.
(1)求证:△ABD≌△CDB;
(2)若∠DBE=37°,求∠ADC的度数.
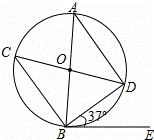
(1)证明:∵AB,CD是直径,
∴∠ADB=∠CBD=90°,
在Rt△ABD和Rt△CDB中,
 ,
,
∴Rt△ABD和Rt△CDB(HL);
(2)解:∵BE是切线,
∴AB⊥BE,
∴∠ABE=90°,
∵∠DBE=37°,
∴∠ABD=53°,
∵OA=OD,
∴∠BAD=∠ODA=90°﹣53°=37°,
∴∠ADC的度数为37°.

练习册系列答案
相关题目
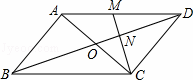
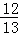 ,DE是水位线,DE∥AB.
,DE是水位线,DE∥AB.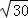 m时,求此时的水深;
m时,求此时的水深;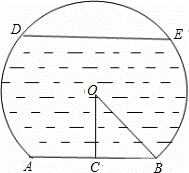



 B.
B. C.
C. D.
D. 

 海里 B.40
海里 B.40 海里 C.80海里 D. 40
海里 C.80海里 D. 40 海里
海里