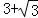题目内容
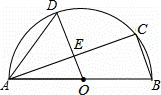
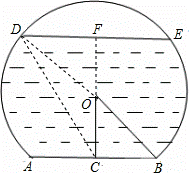
一个弓形桥洞截面示意图如图所示,圆心为O,弦AB是水底线,OC⊥AB,AB=24m,sin∠COB=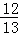 ,DE是水位线,DE∥AB.
,DE是水位线,DE∥AB.
(1)当水位线DE=4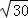 m时,求此时的水深;
m时,求此时的水深;
(2)若水位线以一定的速度下降,当水深8m时,求此时∠ACD的余切值.
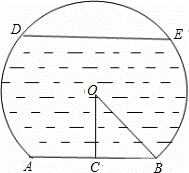
解:(1)延长CO交DE于点F,连接OD
∵OC⊥AB,OC过圆心,AB=24m,
∴BC= AB=12m.
AB=12m.
在Rt△BCO中,sin∠COB=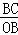 =
=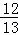 ,
,
∴OB=13mCO=5m.
∵DE∥AB,
∴∠ACD=∠CDE,∠DFO=∠BCO=90°.
又∵OF过圆心,
∴DF=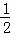 DE=
DE=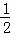 ×4
×4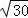 =2
=2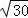 m.
m.
在Rt△DFO中,OF=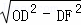 =
=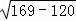 =7m,
=7m,
∴CF=CO+OF=12m,即当水位线DE=4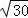 m时,此时的水深为12m;
m时,此时的水深为12m;
(2)若水位线以一定的速度下降,当水深8m时,即CF=8m,则OF=CF﹣OC=3m,
连接CD,在Rt△ODF中,DF=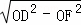 =
=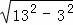 =4
=4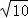 m.
m.
在Rt△CDF中,cot∠CDF=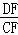 =
=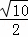 .
.
∵DE∥AB,
∴∠ACD=∠CDE,
∴cot∠ACD=cot∠CDF=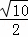 .
.
答:若水位线以一定的速度下降,当水深8m时,此时∠ACD的余切值为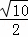 .
.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目


 ,则a的值是( )
,则a的值是( )
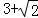 C.
C.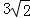 D.
D.