题目内容
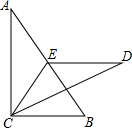 如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,沿△ABC的中线CE将△CBA折叠,使点A落在点D处,若CD恰好与EB垂直,则tanB的值为( )
如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,沿△ABC的中线CE将△CBA折叠,使点A落在点D处,若CD恰好与EB垂直,则tanB的值为( )A、
| ||
B、
| ||
C、
| ||
D、
|
考点:翻折变换(折叠问题)
专题:
分析:根据直角三角形斜边上的中线等于斜边的一半可得CE=AE=
AB,根据等边对等角可得∠A=∠ACE,再根据翻折的性质可得∠ACE=∠DCE,然后根据直角三角形两锐角互余列方程求出∠A=30°,再根据直角三角形两锐角互余求出∠B=60°,然后根据特殊角的三角函数求解即可.
| 1 |
| 2 |
解答:解:∵CE是Rt△ABC的中线,
∴CE=AE=
AB,
∴∠A=∠ACE,
由翻折的性质得,∠ACE=∠DCE,
∵CD⊥EB,
∴∠A+∠ACE+∠DCE=90°,
∴∠A=30°,
∴∠B=90°-30°=60°,
∴tanB=tan60°=
.
故选B.
∴CE=AE=
| 1 |
| 2 |
∴∠A=∠ACE,
由翻折的性质得,∠ACE=∠DCE,
∵CD⊥EB,
∴∠A+∠ACE+∠DCE=90°,
∴∠A=30°,
∴∠B=90°-30°=60°,
∴tanB=tan60°=
| 3 |
故选B.
点评:本题考查了翻折变换的性质,直角三角形斜边上的中线等于斜边的一半的性质,熟记各性质并求出∠A=30°是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,△ABC≌△BAD,A和B,C和D是对应顶点,如果AB=6cm,BD=5cm,AD=4cm,那么BC等于( )
如图,△ABC≌△BAD,A和B,C和D是对应顶点,如果AB=6cm,BD=5cm,AD=4cm,那么BC等于( )| A、6cm | B、5cm |
| C、4cm | D、5cm或4cm |
过A、B、C三点,最多可确定直线的条数是( )
| A、1条 | B、3条 |
| C、1条或2条 | D、1条或3条 |
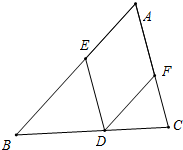 菱形AEDF内接于△ABC,且AB=21cm,AC=15cm,BC=18cm,求BD,CD及菱形的边长.
菱形AEDF内接于△ABC,且AB=21cm,AC=15cm,BC=18cm,求BD,CD及菱形的边长. 直角三角形纸片的两直角边长分别为6,8,现将△ABC如图那样折叠,使点A与点B重合,折痕为DE,则
直角三角形纸片的两直角边长分别为6,8,现将△ABC如图那样折叠,使点A与点B重合,折痕为DE,则