题目内容
4.若函数y=(a-1)x2-2x+a的图象与坐标轴有两个交点,求a的值.分析 由于该函数没有说明是二次函数,故a-1应分两种情况进行讨论.
解答 解:(1)当a-1=0,即a=1时,函数为一次函数y=-2x+1,符合题意.
(2)当a-1≠0,即a≠1时,函数为二次函数
①图象与x轴只有一个交点.此时△=0
∴4-4a(a-1)=0,
解得:a=$\frac{1±\sqrt{5}}{2}$,
此时抛物线与x轴、y轴各有一个交点,符合题意,
②图象过原点(0,0)代入y=(a-1)x2-2x+a,得a=0,
∴综上所述,a=1或a=0或$a=\frac{{1+\sqrt{5}}}{2}或{a_{\;}}=\frac{{1-\sqrt{5}}}{2}$
点评 本题考查二次函数与x轴的交点问题,涉及一元二次方程的解法,一次函数图象的性质.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
12.下列说法中,不正确的是( )
| A. | 同角的余角相等 | |
| B. | 两直线平行,同旁内角相等 | |
| C. | 在同一平面内,不相交的两条直线叫平行线 | |
| D. | 对顶角相等 |
19. 如图,在△ABC中,∠CAB=67°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
如图,在△ABC中,∠CAB=67°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
 如图,在△ABC中,∠CAB=67°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
如图,在△ABC中,∠CAB=67°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )| A. | 46° | B. | 50° | C. | 65° | D. | 67° |
13.已知等腰三角形一腰上的中线将它的周长分成9cm和12cm两部分,则等腰三角形的底边长为( )
| A. | 9cm | B. | 5cm | C. | 6cm或5cm | D. | 5cm或9cm |
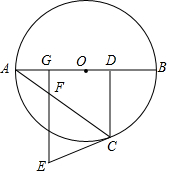 如图,AB是圆O之间,C是圆O上一点,过C作CD⊥AB于D,EC与圆O相切于C且CE=CD.
如图,AB是圆O之间,C是圆O上一点,过C作CD⊥AB于D,EC与圆O相切于C且CE=CD.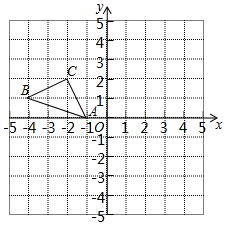 正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
 如图,在Rt△ABC中,∠ACB=90°,∠A=40°,以直角顶点C为旋转中心,将△ABC旋转到△A′B′C的位置,其中A′、B′分别是A、B的对应点,且点B在斜边A′B′上,直角边CA′交AB于D,则旋转角等于( )
如图,在Rt△ABC中,∠ACB=90°,∠A=40°,以直角顶点C为旋转中心,将△ABC旋转到△A′B′C的位置,其中A′、B′分别是A、B的对应点,且点B在斜边A′B′上,直角边CA′交AB于D,则旋转角等于( )