题目内容
6.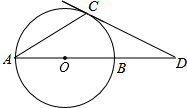 如图,已知在⊙0中,直径AB与弦AC的夹角是30°,过C点的切线交AB的延长线于D,AC=$\sqrt{6}$cm,求CD的长.
如图,已知在⊙0中,直径AB与弦AC的夹角是30°,过C点的切线交AB的延长线于D,AC=$\sqrt{6}$cm,求CD的长.
分析 连接OC.由等腰三角形的性质得到∠ACO=∠A=30°,根据三角形的外角的性质得到∠COD=∠A+∠ACO=60°,根据切线的性质得到∠OCD=90°,求得∠A=∠D,根据等腰三角形的性质即可得到结论.
解答  解:连接OC.
解:连接OC.
∵OA=OC,
∴∠ACO=∠A=30°,
∴∠COD=∠A+∠ACO=60°,
∵CD是圆的切线,
∴∠OCD=90°,
∴∠D=30°,
∴∠A=∠D,
∴CD=AC=$\sqrt{6}$.
点评 本题考查了切线的性质定理,等腰三角形的判定和性质,运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
相关题目
14. 如图,在△ABC中,AB=AC,P为△ABC的中线AD上任意一点,若点P到边AB的距离为2cm,则点P到边AC的距离为( )
如图,在△ABC中,AB=AC,P为△ABC的中线AD上任意一点,若点P到边AB的距离为2cm,则点P到边AC的距离为( )
 如图,在△ABC中,AB=AC,P为△ABC的中线AD上任意一点,若点P到边AB的距离为2cm,则点P到边AC的距离为( )
如图,在△ABC中,AB=AC,P为△ABC的中线AD上任意一点,若点P到边AB的距离为2cm,则点P到边AC的距离为( )| A. | 1cm | B. | 1.5cm | C. | 2cm | D. | 2.5cm |
1.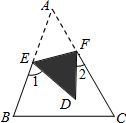 如图,△ABC中,∠A=50°,点E、F在AB、AC上,沿EF向内折叠△AEF,得△DEF,则图中∠1+∠2等于( )
如图,△ABC中,∠A=50°,点E、F在AB、AC上,沿EF向内折叠△AEF,得△DEF,则图中∠1+∠2等于( )
 如图,△ABC中,∠A=50°,点E、F在AB、AC上,沿EF向内折叠△AEF,得△DEF,则图中∠1+∠2等于( )
如图,△ABC中,∠A=50°,点E、F在AB、AC上,沿EF向内折叠△AEF,得△DEF,则图中∠1+∠2等于( )| A. | 130° | B. | 120° | C. | 65° | D. | 100° |
18.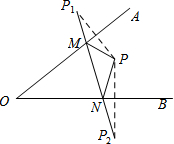 如图,∠AOB内一点P,P1,P2分别是P关于OA、OB的对称点,P1P2交OA于点M,交OB于点N.若△PMN的周长是5cm,则P1P2的长为( )
如图,∠AOB内一点P,P1,P2分别是P关于OA、OB的对称点,P1P2交OA于点M,交OB于点N.若△PMN的周长是5cm,则P1P2的长为( )
 如图,∠AOB内一点P,P1,P2分别是P关于OA、OB的对称点,P1P2交OA于点M,交OB于点N.若△PMN的周长是5cm,则P1P2的长为( )
如图,∠AOB内一点P,P1,P2分别是P关于OA、OB的对称点,P1P2交OA于点M,交OB于点N.若△PMN的周长是5cm,则P1P2的长为( )| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
15.已知y=(m+1)${x}^{{m}^{2}}$,如果y是x的正比例函数,则m的值为( )
| A. | 1 | B. | -1 | C. | 1,-1 | D. | 0 |
 如图,在菱形ABCD中,对角线AC、BD相交于点O,∠BAD=120°,AC=8cm,则菱形ABCD面积是32$\sqrt{3}$ cm2.
如图,在菱形ABCD中,对角线AC、BD相交于点O,∠BAD=120°,AC=8cm,则菱形ABCD面积是32$\sqrt{3}$ cm2.