Question

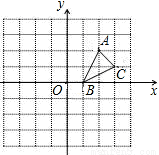
如图，已知△ABC，过A点作AD∥BC,DF和AC交于E点，且AD=CF，连BE.

（1）证明：E是DF中点;

（2）若,°,证明:是等边三角形

 

Answer 1

（1）证明见解析；（2）证明见解析.

【解析】

试题分析：（1）由条件易证△ADE≌△CFE，所以AE=CE，从而可证E是DF中点;

（2）由（1）可得AE=CE，又，得是等腰三角形，由于，所以可证是等边三角形.

试题解析：（1）证明：∵

∴∠ADE=∠CFE, ∠DAE=∠FCE,

又∵

∴△ADE≌△CFE（ASA）

∴DE=FE

∴是中点

（2）证明：已证明△ADE≌△CFE

∴AE=CE

又∵

∴BE是AC的垂直平分线

∴BA=BC

∴是等腰三角形

又∵

∴等腰是等边三角形

考点：1.全等三角形的判定与性质；2.等边三角形的判定.