题目内容
3. 如图,在等腰直角三角形ABC中,∠ABC=90°,D为边AC的中点,过点D作DE⊥DF,交AB于点E,交BC于点F,连接EF,若AE=4,FC=3,求EF的长.
如图,在等腰直角三角形ABC中,∠ABC=90°,D为边AC的中点,过点D作DE⊥DF,交AB于点E,交BC于点F,连接EF,若AE=4,FC=3,求EF的长.
分析 连接BD,根据的等腰直角三角形的性质证明△BED≌△CFD就可以得出AE=BF、BE=CF,由AE=BF,FC=BE就可以求得EF的长.
解答 解:连接BD.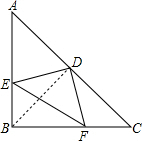
∵D是AC中点,
∴∠ABD=∠CBD=45°,BD=AD=CD,BD⊥AC
∵∠EDB+∠FDB=90°,∠FDB+∠CDF=90°,
∴∠EDB=∠CDF,
在△BED和△CFD中,
∵$\left\{\begin{array}{l}{∠EBD=∠C}\\{BD=CD}\\{∠EDB=∠CDF}\end{array}\right.$,
∴△BED≌△CFD(ASA),
∴BE=CF;
∵AB=BC,BE=CF=3,
∴AE=BF=4,
在Rt△BEF中,EF=$\sqrt{B{E}^{2}+B{F}^{2}}$=5.
点评 本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,考查了勾股定理的运用,本题中连接BD证得△BED≌△CFD是解题的关键.

练习册系列答案
相关题目
11.下列方程属于一元一次方程的是( )
| A. | 3x+2y=13 | B. | x2-x=1 | C. | x-$\frac{1}{x}$=0 | D. | x+4=2-2x |
18.若m>n,则下列各式正确的是( )
| A. | 2m-2n<0 | B. | m-3>n-3 | C. | -3m>-3n | D. | $\frac{m}{2}$<$\frac{n}{2}$ |
12.下列方程中,一元二次方程的是( )
| A. | x2+$\frac{1}{{x}^{2}}$=0 | B. | (2x+1)(x-3)=1 | C. | ax2+bx=0 | D. | 3x2-2xy-5y2=0 |
 如图所示,AB∥CD,AD∥BC,∠1=65°,∠2=55°,求∠C的度数60°.
如图所示,AB∥CD,AD∥BC,∠1=65°,∠2=55°,求∠C的度数60°. 如图,OD=OC,要使△AOD≌△BOC,需添加的一个条件是∠D=∠C(添一个条件即可)
如图,OD=OC,要使△AOD≌△BOC,需添加的一个条件是∠D=∠C(添一个条件即可)