题目内容
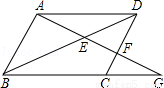
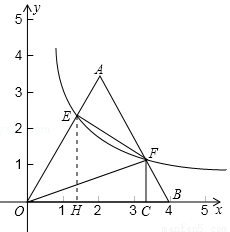
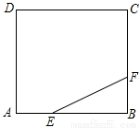
如图,将边长为4的等边三角形AOB放置于平面直角坐标系xOy中,F是AB边上的动点(不与点A,B重合),过点F的反比例函数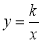 (
(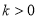 ,
,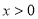 )与OA边交于点E,过点F作FC⊥x轴于点C,连接EF,OF.
)与OA边交于点E,过点F作FC⊥x轴于点C,连接EF,OF.

(1)若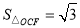 ,求反比例函数的解析式;
,求反比例函数的解析式;
(2)在(1)的条件下,试判断以点E为圆心,EA长为半径的圆与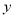 轴的位置关系,并说明理由;
轴的位置关系,并说明理由;
(3)AB边上是否存在点F,使得EF⊥AE?若存在,请求出BF:FA的值;若不存在,请说明理由.
(1)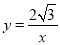 (
(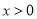 );(2)相离;(3)存在,1:4.
);(2)相离;(3)存在,1:4.
【解析】
试题分析:(1)设F(x,y),得到OC=x与CF=y,表示出三角形OCF的面积,求出xy的值,即为k的值,进而确定出反比例解析式;
(2)过E作EH垂直于x轴,EG垂直于y轴,设OH为m,利用等边三角形的性质及锐角三角函数定义表示出EH与OE,进而表示出E的坐标,代入反比例解析式中求出m的值,确定出EG,OE,EH的长,根据EA与EG的大小关系即可对于圆E与y轴的位置关系作出判断;
(3)过E作EH垂直于x轴,设FB=x,利用等边三角形的性质及锐角三角函数定义表示出FC与BC,进而表示出AF与OC,表示出AE与OE的长,得出OE与EH的长,表示出E与F坐标,根据E与F都在反比例图象上,得到横纵坐标乘积相等列出方程,求出方程的解得到x的值,即可求出BF与FA的比值.
试题解析:(1)设F(x,y),(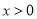 ,
,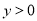 ),则OC=x,CF=y,∴
),则OC=x,CF=y,∴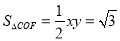 ,∴
,∴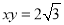 ,∴
,∴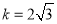 ,∴反比例函数解析式为
,∴反比例函数解析式为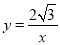 (
(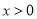 );
);
(2)该圆与y轴相离,理由为:过点E作EH⊥x轴,垂足为H,过点E作EG⊥y轴,垂足为G,
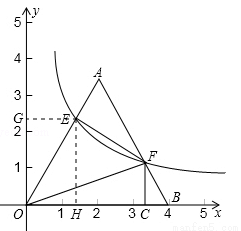
在△AOB中,OA=AB=4,∠AOB=∠ABO=∠A=60°,设OH=m,则tan∠AOB=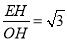 ,∴EH=
,∴EH=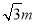 ,OE=2m,∴E坐标为(m,
,OE=2m,∴E坐标为(m,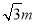 ),∵E在反比例
),∵E在反比例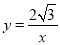 图象上,∴
图象上,∴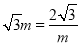 ,∴
,∴ ,
,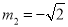 (舍去),∴OE=
(舍去),∴OE=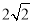 ,EA=
,EA=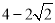 ,EG=
,EG=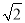 ,∵
,∵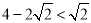 ,∴EA<EG,∴以E为圆心,EA长为半径的圆与y轴相离;
,∴EA<EG,∴以E为圆心,EA长为半径的圆与y轴相离;
(3)存在.假设存在点F,使AE⊥FE,过E点作EH⊥OB于点H,设BF=x.∵△AOB是等边三角形,∴AB=OA=OB=4,∠AOB=∠ABO=∠A=60°,∴BC=FBcos∠FBC=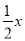 ,FC=FBsin∠FBC=
,FC=FBsin∠FBC=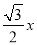 ,∴AF=4﹣x,OC=OB﹣BC=
,∴AF=4﹣x,OC=OB﹣BC=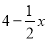 ,∵AE⊥FE,∴AE=AFcosA=
,∵AE⊥FE,∴AE=AFcosA=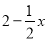 ,∴OE=OA﹣AE=
,∴OE=OA﹣AE=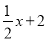 ,∴OH=OEcos∠AOB=
,∴OH=OEcos∠AOB=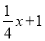 ,EH=OEsin∠AOB=
,EH=OEsin∠AOB=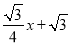 ,∴E(
,∴E(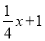 ,
,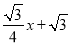 ),F(
),F(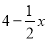 ,
,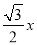 ),∵E、F都在双曲线
),∵E、F都在双曲线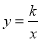 的图象上,∴(
的图象上,∴(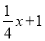 )(
)(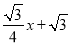 )=(
)=(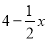 )
)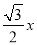 ,解得:
,解得: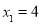 ,
,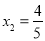 ,当BF=4时,AF=0,
,当BF=4时,AF=0,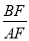 不存在,舍去;当BF=
不存在,舍去;当BF=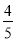 时,AF=
时,AF=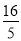 ,BF:AF=1:4.
,BF:AF=1:4.
考点:反比例函数综合题.

 一架梯子斜靠在墙上,若梯子底端到墙的距离AC=3米,cos∠B
一架梯子斜靠在墙上,若梯子底端到墙的距离AC=3米,cos∠B AC=
AC= ,则梯子AB的长度为 米.
,则梯子AB的长度为 米.

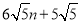 B.
B.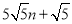 C.
C. D.
D.
 BC,求:
BC,求: