题目内容
如图,在平行四边形ABCD中,点G是BC延长线上一点,AG与BD交于点E,与DC交于点F,如果AB=m,CG=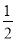 BC,求:
BC,求:
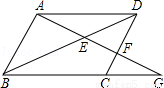
(1)DF的长度;
(2)三角形ABE与三角形FDE的面积之比.
(1) ;(2)9:4.
;(2)9:4.
【解析】
试题分析:(1)先根据平行四边形的性质和已知关系,得出CG和BG之间的关系,即CG= BG,和
BG,和 ,即可得出
,即可得出 .
.
(2)根据平行线的性质,由AB∥CD,课得出△ABE∽△FDE,再根据相似三角形的性质,面积比等于相似比的平方,即 ,即得△ABE与△FDE的面积之比为9:4.
,即得△ABE与△FDE的面积之比为9:4.
试题解析:(1)∵四边形ABCD是平行四边形,∴AB=CD=m,AB∥CD,∵CG= BC,∴CG=
BC,∴CG= BG,∵AB∥CD,∴
BG,∵AB∥CD,∴ ,∴
,∴ ,∴
,∴ ;
;
(2)∵AB∥CD,∴△ABE∽△FDE,∴ ,∴△ABE与△FDE的面积之比为9:4.
,∴△ABE与△FDE的面积之比为9:4.

考点:1.相似三角形的判定与性质;2.平行四边形的性质.

练习册系列答案
相关题目
 中,
中, ,
, ,
, ,则
,则
 .
.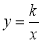 (
(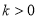 ,
,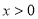 )与OA边交于点E,过点F作FC⊥x轴于点C,连接EF,OF.
)与OA边交于点E,过点F作FC⊥x轴于点C,连接EF,OF.
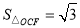 ,求反比例函数的解析式;
,求反比例函数的解析式;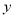 轴的位置关系,并说明理由;
轴的位置关系,并说明理由; 的一个根,则这个方程的另一个根是( )
的一个根,则这个方程的另一个根是( )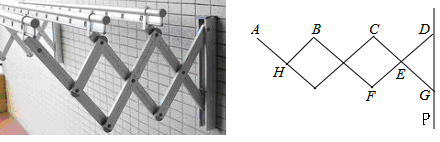
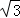 ≈1.732)
≈1.732)
 和
和 (
( )在同一坐标系中的图象大致是( )
)在同一坐标系中的图象大致是( ) B.
B. C.
C. D.
D.

 )]×[-10+
)]×[-10+ ]
]