题目内容
甲乙两人玩一种游戏:三张大小、质地都相同的卡片上分别标有数字1,2,3,现将标有数字的一面朝下,洗匀后甲从中任意抽取一张,记下数字后放回;又将卡片洗匀,乙也从中任意抽取一张,计算甲乙两人抽得的两个数字之积,如果积为奇数则甲胜,若积为偶数则乙胜.
(1)用列表或画树状图等方法,列出甲乙两人抽得的数字之积所有可能出现的情况;
(2)请判断该游戏对甲乙双方是否公平?并说明理由.
1,2,3,2,4,6,3,6,9,共9种;不公平. 【解析】 试题分析:(1)列表得出所有等可能的情况数,找出甲乙两人抽得的数字之积所有可能出现的情况即可; (2)分别求出甲乙两人获胜的概率,比较即可得到结果. 试题解析:(1)列表如下: 1 2 3 1 (1,1) (2,1) (3,1) 2 (1,2) ...
练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.
(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A.请完成下列表格:
事件A | 必然事件 | 随机事件 |
m的值 |
(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个球是黑球的可能性大小是 ,求m的值.
,求m的值.


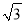 B.
B. 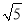 C.
C. 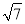 D. 3
D. 3
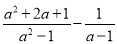 进行化简,然后请你选择一个合适
进行化简,然后请你选择一个合适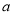 的值,并求代数式的值.
的值,并求代数式的值.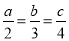 ,则
,则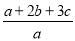 等于( )
等于( )