题目内容
7.计算:(1)$\sqrt{45}$-$\sqrt{20}$
(2)$\sqrt{27}$×$\sqrt{50}$÷$\sqrt{6}$.
分析 (1)先化简题目中的二次根式,然后根据二次根式的减法即可解答本题;
(2)根据二次根式的乘除法可以解答本题.
解答 解:(1)$\sqrt{45}$-$\sqrt{20}$
=$3\sqrt{5}-2\sqrt{5}$
=$\sqrt{5}$;
(2)$\sqrt{27}$×$\sqrt{50}$÷$\sqrt{6}$
=$3\sqrt{3}×5\sqrt{2}×\frac{1}{\sqrt{6}}$
=15.
点评 本题考查二次根式的混合运算,解答本题的关键是明确二次根式的混合运算的解答方法.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
15.一次函数y=kx+1的图象必过点( )
| A. | (0,1) | B. | (0,-1) | C. | (1,0) | D. | (-1,0) |
2.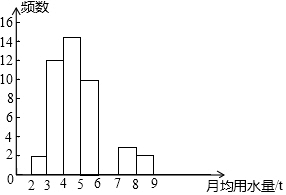 小明同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了若干居民的月均用水量(单位:t),并绘制了不完整的样本的频数分布表的频数分布直方图(如图)
小明同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了若干居民的月均用水量(单位:t),并绘制了不完整的样本的频数分布表的频数分布直方图(如图)
根据上述图表回答下列问题:
(1)小明同学共调查了多少户居民的月均用水量;
(2)请根据题中已有的信息补全频数分布表和频数分布直方图;
(3)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你通过样本估计总体中的等用水量家庭大约有多少户?
 小明同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了若干居民的月均用水量(单位:t),并绘制了不完整的样本的频数分布表的频数分布直方图(如图)
小明同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了若干居民的月均用水量(单位:t),并绘制了不完整的样本的频数分布表的频数分布直方图(如图)根据上述图表回答下列问题:
| 月均用水量(单位:t) | 频数 | 百分比 |
| 2≤x<3 | 2 | 0.04 |
| 3≤x<4 | 12 | 0.24 |
| 4≤x<5 | 15 | 0.3 |
| 5≤x<6 | 10 | 0.2 |
| 6≤x<7 | 6 | 0.12 |
| 7≤x<8 | 3 | 0.06 |
| 8≤x<9 | 2 | 0.04 |
(2)请根据题中已有的信息补全频数分布表和频数分布直方图;
(3)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你通过样本估计总体中的等用水量家庭大约有多少户?
19.观察下列图形:它们是按一定的规律排列,依照此规律第n个图形共有( )个五角星.

| A. | 1+n | B. | 1+2n | C. | 2+n | D. | 1+3n |
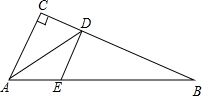 如图,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,点E是AB上任意一点.若CD=5,则DE的最小值等于( )
如图,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,点E是AB上任意一点.若CD=5,则DE的最小值等于( )
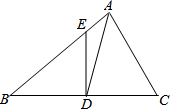 如图,在△ABC中,∠B=35°,∠C=65°,AD平分∠BAC,过点D作BC的垂线,交AB于点E,求∠ADE的度数.请完成剩下的解答过程.
如图,在△ABC中,∠B=35°,∠C=65°,AD平分∠BAC,过点D作BC的垂线,交AB于点E,求∠ADE的度数.请完成剩下的解答过程.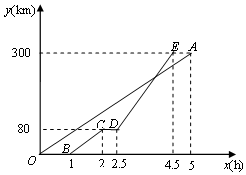 甲、乙两地相距300km,一辆货车和一辆轿车先后从甲地出发向乙地.如图,线段OA表示货车离甲地距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地距离y(km)与时间x(h)之间的函数关系.请根据图象,解答下列问题:
甲、乙两地相距300km,一辆货车和一辆轿车先后从甲地出发向乙地.如图,线段OA表示货车离甲地距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地距离y(km)与时间x(h)之间的函数关系.请根据图象,解答下列问题: