题目内容
19.新农村社区改造中,有一部分楼盘要对外销售,某楼盘共23层,销售价格如下:第八层楼房售价为4000元/米2,从第八层起每上升一层,每平方米的售价提高50元;反之,楼层每下降一层,每平方米的售价降低30元,已知该楼盘每套楼房面积均为120米2.若购买者一次性付清所有房款,开发商有两种优惠方案:
方案一:降价8%,另外每套楼房赠送a元装修基金;
方案二:降价10%,没有其他赠送.
(1)请写出售价y(元/米2)与楼层x(1≤x≤23,x取整数)之间的函数关系式;
(2)老王要购买第十六层的一套楼房,若他一次性付清购房款,请帮他计算哪种优惠方案更加合算.
分析 (1)根据题意分别求出当1≤x≤8时,每平方米的售价应为4000-(8-x)×30元,当9≤x≤23时,每平方米的售价应为4000+(x-8)×50元;
(2)根据购买方案一、二求出实交房款的关系式,然后分情况讨论即可确定那种方案合算.
解答 解:(1)当1≤x≤8时,每平方米的售价应为:
y=4000-(8-x)×30=30x+3760 (元/平方米)
当9≤x≤23时,每平方米的售价应为:
y=4000+(x-8)×50=50x+3600(元/平方米).
∴y=$\left\{\begin{array}{l}{30x+3760(1≤x≤8)}\\{50x+3600(9≤x≤23)}\end{array}\right.$
(2)第十六层楼房的每平方米的价格为:50×16+3600=4400(元/平方米),
按照方案一所交房款为:W1=4400×120×(1-8%)-a=485760-a(元),
按照方案二所交房款为:W2=4400×120×(1-10%)=475200(元),
当W1>W2时,即485760-a>475200,
解得:0<a<10560,
当W1=W2时,即485760-a=475200,
解得:a=10560
当W1<W2时,即485760-a<475200,
解得:a>10560,
∴当0<a<10560时,方案二合算;当a>10560时,方案一合算.当a=10560时,方案一与方案二一样.
点评 本题考查的是用一次函数解决实际问题,读懂题目信息,找出数量关系表示出各楼层的单价以及是交房款的关系式是解题的关键.

练习册系列答案
相关题目
10.以下四个选项表示某天四个城市的平均气温,其中平均气温最低的是( )
| A. | -3℃ | B. | 15℃ | C. | -10℃ | D. | -1℃ |
7.某市6月某周内每天的最高气温数据如下(单位:℃):
24 26 29 26 29 32 29
则这组数据的众数和中位数分别是( )
24 26 29 26 29 32 29
则这组数据的众数和中位数分别是( )
| A. | 29,29 | B. | 26,26 | C. | 26,29 | D. | 29,32 |
14.要将抛物线y=x2+2x+3平移后得到抛物线y=x2,下列平移方法正确的是( )
| A. | 向左平移1个单位,再向上平移2个单位 | |
| B. | 向左平移1个单位,再向下平移2个单位 | |
| C. | 向右平移1个单位,再向上平移2个单位 | |
| D. | 向右平移1个单位,再向下平移2个单位 |
4.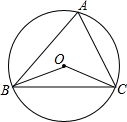 如图,圆O是△ABC的外接圆,∠A=68°,则∠OBC的大小是( )
如图,圆O是△ABC的外接圆,∠A=68°,则∠OBC的大小是( )
 如图,圆O是△ABC的外接圆,∠A=68°,则∠OBC的大小是( )
如图,圆O是△ABC的外接圆,∠A=68°,则∠OBC的大小是( )| A. | 22° | B. | 26° | C. | 32° | D. | 68° |
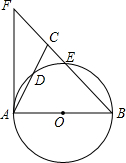 如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线于⊙O的切线AF交于点F.
如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线于⊙O的切线AF交于点F.