Question

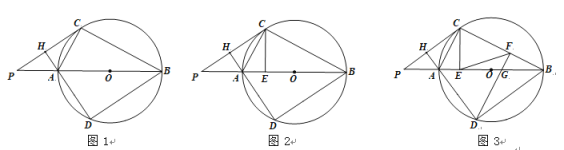
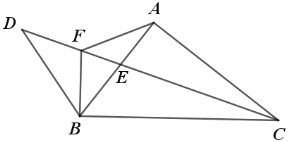
【题目】如图，Rt△ABC 中，∠BAC=90°，CE 平分∠ACB，点 D 在 CE的延长线上，连接 BD，过B作BF⊥BC交 CD 于点 F，连接 AF，若CF=2BD ，DE：CE=5：8 ， BF ，则AF的长为_________．

Answer 1

【答案】

【解析】

取CF的中点为M连接BM，可证得与均为等腰三角形，设，通过角的计算可证得与均为等腰三角形，由，设，过B作于N，过A作于G，根据相似三角形的性质结合勾股定理可求得的值以及AG、FG的值，利用勾股定理即可求解．

取CF的中点为M连接BM，

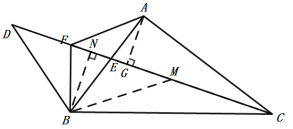
∵BF⊥BC，

∴∠FBC=90，

∴CM=FM=BM==BD，

∴与均为等腰三角形，

，

设，则，，

，

，

∴可得与均为等腰三角形，

∵，

设，则，，，

∴，

过B作于N，过A作于G，

得，，

∵∠FBN+∠BFN=90，∠FCB+∠BFN=90，

∴∠FBN=∠FCB，

∴△RtFBNRt△BCN，

∴，

∴,

∴，

∴，

∵，

∴，

∴，，，，

∵∠BEN=∠CEA，

∴Rt△BENRt△CEA，

∴，即，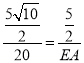

∴,

∵∠BEN=∠AEG，

∴Rt△BENRt△AEG，

∴，即，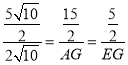

∴，，

∴，

在Rt△AFG中，

．