Question

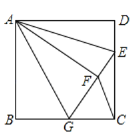
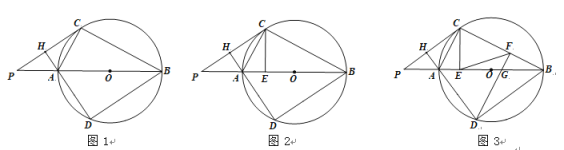
【题目】在⊙O 中，AB 为直径，点 P 在BA 的延长线上，PC 为⊙O 的切线，过点 A 作AH⊥PC 于点 H， 交⊙O 于点 D，连接 BC、BD、AC．

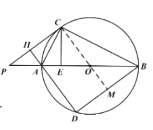
(1)如图 1，求证：∠CAH=∠CAB；

(2)如图 2，过点 C 作 CE⊥AB 于点 E，求证：BD=2CE；

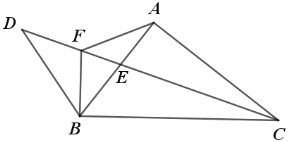
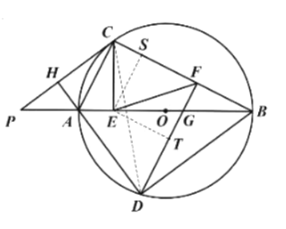
(3)如图 3，在(2)的条件下，点 F 在BC 上，连接 DF、EF，若 BG=2AE，∠CFE=45°，OG=1，求线段 EF 的长．

Answer 1

【答案】（1）见解析；（2）见解析；（3）．

【解析】

（1）连接OC，根据切线的性质证得，利用半径相等即可证明；

（2）延长CO交BD于点M，根据角平分线的性质证得，证得四边形为矩形，推出，，，利用垂径定理即可证明；

（3）连接CD，过点E作于点，于点，设，则，，由，推出，，即，再推出，证得，得到，在中，利用勾股定理求得，然后解直角三角形即可求解．

（1）证明：连接OC，

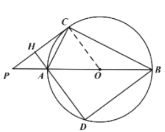
∵PC为圆O的切线，

∴，，

∵，

∴，

∴，

∴，

∵，

∴，

∴；

（2）证明：连接OC，延长CO交BD于点M，

∵，，，

∴，

∵AB为直径，

∴，

∴，

∴四边形为矩形，

∴，，，

∴；

（3）解：连接CD，过点E作于点，于点，

在和中，

∵，，

∴

∴，

∵，

∴，

∵，，

∴，

∴，

∵，

∴设，则，，

∵，

∴，，，，，，

∴，

∴，

∵，，

∵，

∴，

∴，

∵AB为圆O的直径，

∴，

∴，

∵，

∴，

∵，，

∴，，

∵，

∴，

∵，

∴，

∴，

∴，

在中，，，，

由勾股定理得：，即，

解得：，（舍去）

∴，，

∴，

∴，

在Rt△BSE中，，，

，

∴，

在Rt△FSE中，，，

∴．