题目内容
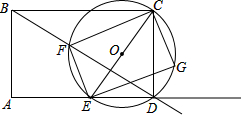 如图,矩形ABCD的边AB=3cm,AD=4cm,点E从点A出发,沿射线AD移动,以CE为直径作圆O,点F为圆O与射线BD的公共点,连接EF、CF,过点E作EG⊥EF,EG与圆O相交于点G,连接CG.
如图,矩形ABCD的边AB=3cm,AD=4cm,点E从点A出发,沿射线AD移动,以CE为直径作圆O,点F为圆O与射线BD的公共点,连接EF、CF,过点E作EG⊥EF,EG与圆O相交于点G,连接CG.(1)试说明四边形EFCG是矩形;
(2)当圆O与射线BD相切时,点E停止移动,在点E移动的过程中,
①矩形EFCG的面积是否存在最大值或最小值?若存在,求出这个最大值或最小值;若不存在,说明理由;
②求点G移动路线的长.
考点:圆的综合题
专题:压轴题,存在型
分析:(1)只要证到三个内角等于90°即可.
(2)易证点D在⊙O上,根据圆周角定理可得∠FCE=∠FDE,从而证到△CFE∽△DAB,根据相似三角形的性质可得到S矩形EFCG=2S△CFE=
.然后只需求出CF的范围就可求出S矩形EFCG的范围.根据圆周角定理和矩形的性质可证到∠GDC=∠FDE=定值,从而得到点G的移动的路线是线段,只需找到点G的起点与终点,求出该线段的长度即可.
(2)易证点D在⊙O上,根据圆周角定理可得∠FCE=∠FDE,从而证到△CFE∽△DAB,根据相似三角形的性质可得到S矩形EFCG=2S△CFE=
| 3CF2 |
| 4 |
解答:解:(1) 证明:如图1,
证明:如图1,
∵CE为⊙O的直径,
∴∠CFE=∠CGE=90°.
∵EG⊥EF,
∴∠FEG=90°.
∴∠CFE=∠CGE=∠FEG=90°.
∴四边形EFCG是矩形.
(2)①存在.
连接OD,如图2①,
∵四边形ABCD是矩形,
∴∠A=∠ADC=90°.
∵点O是CE的中点,
∴OD=OC.
∴点D在⊙O上.
∵∠FCE=∠FDE,∠A=∠CFE=90°,
∴△CFE∽△DAB.
∴
=(
)2.
∵AD=4,AB=3,
∴BD=5,
S△CFE=(
)2•S△DAB
=
×
×3×4
=
.
∴S矩形EFCG=2S△CFE
=
.
∵四边形EFCG是矩形,
∴FC∥EG.
∴∠FCE=∠CEG.
∵∠GDC=∠CEG,∠FCE=∠FDE,
∴∠GDC=∠FDE.
∵∠FDE+∠CDB=90°,
∴∠GDC+∠CDB=90°.
∴∠GDB=90°
Ⅰ.当点E在点A(E′)处时,点F在点B(F′)处,点G在点D(G′)处,如图2①所示.
此时,CF=CB=4.
Ⅱ.当点F在点D(F″)处时,直径F″G″⊥BD,
如图2②所示,
此时⊙O与射线BD相切,CF=CD=3.
Ⅲ.当CF⊥BD时,CF最小,
如图2③所示.
S△BCD=
BC•CD=
BD•CF
∴4×3=5×CF
∴CF=
.
∴
≤CF≤4.
∵S矩形EFCG=
,
∴
×(
)2≤S矩形EFCG≤
×42.
∴
≤S矩形EFCG≤12.
∴矩形EFCG的面积最大值为12,最小值为
.
②∵∠GDC=∠FDE=定值,点G的起点为D,终点为G″,如图2②所示,
∴点G的移动路线是线段DG″.
∵∠G″DC=∠BDA,∠DCG″=∠A=90°,
∴△DCG″∽△DAB.
∴
=
.
∴
=
.
∴DG″=
.
∴点G移动路线的长为
.
 证明:如图1,
证明:如图1,∵CE为⊙O的直径,
∴∠CFE=∠CGE=90°.
∵EG⊥EF,
∴∠FEG=90°.
∴∠CFE=∠CGE=∠FEG=90°.
∴四边形EFCG是矩形.
(2)①存在.
连接OD,如图2①,
∵四边形ABCD是矩形,
∴∠A=∠ADC=90°.
∵点O是CE的中点,
∴OD=OC.
∴点D在⊙O上.
∵∠FCE=∠FDE,∠A=∠CFE=90°,
∴△CFE∽△DAB.
∴
| S△CFE |
| S△DAB |
| CF |
| DA |
∵AD=4,AB=3,
∴BD=5,

S△CFE=(
| CF |
| 4 |
=
| CF2 |
| 16 |
| 1 |
| 2 |
=
| 3CF2 |
| 8 |
∴S矩形EFCG=2S△CFE
=
| 3CF2 |
| 4 |
∵四边形EFCG是矩形,
∴FC∥EG.
∴∠FCE=∠CEG.
∵∠GDC=∠CEG,∠FCE=∠FDE,
∴∠GDC=∠FDE.
∵∠FDE+∠CDB=90°,
∴∠GDC+∠CDB=90°.
∴∠GDB=90°

Ⅰ.当点E在点A(E′)处时,点F在点B(F′)处,点G在点D(G′)处,如图2①所示.
此时,CF=CB=4.
Ⅱ.当点F在点D(F″)处时,直径F″G″⊥BD,
如图2②所示,
此时⊙O与射线BD相切,CF=CD=3.
Ⅲ.当CF⊥BD时,CF最小,
如图2③所示.
S△BCD=
| 1 |
| 2 |
| 1 |
| 2 |

∴4×3=5×CF
∴CF=
| 12 |
| 5 |
∴
| 12 |
| 5 |
∵S矩形EFCG=
| 3CF2 |
| 4 |
∴
| 3 |
| 4 |
| 12 |
| 5 |
| 3 |
| 4 |
∴
| 108 |
| 25 |
∴矩形EFCG的面积最大值为12,最小值为
| 108 |
| 25 |
②∵∠GDC=∠FDE=定值,点G的起点为D,终点为G″,如图2②所示,
∴点G的移动路线是线段DG″.

∵∠G″DC=∠BDA,∠DCG″=∠A=90°,
∴△DCG″∽△DAB.
∴
| DC |
| DA |
| DG″ |
| DB |
∴
| 3 |
| 4 |
| DG″ |
| 5 |
∴DG″=
| 15 |
| 4 |
∴点G移动路线的长为
| 15 |
| 4 |
点评:本题考查了矩形的判定与性质、相似三角形的判定与性质、圆周角定理、直角三角形斜边上的中线等于斜边的一半、垂线段定理等知识,考查了动点的移动的路线长,综合性较强.而发现∠CDG=∠ADB及∠FCE=∠ADB是解决本题的关键.

练习册系列答案
相关题目
已知一个正多边形的每个内角都是144°,则该正多边形的边数是( )
| A、7 | B、8 | C、9 | D、10 |

 如图,在边长为1的小正方形组成的方格纸上,将△ABC绕着点A顺时针旋转90°
如图,在边长为1的小正方形组成的方格纸上,将△ABC绕着点A顺时针旋转90°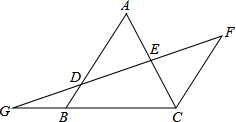 如图,AB∥FC,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于点G.
如图,AB∥FC,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于点G. 如图,直线a,b被直线c所截,a∥b,∠1=∠2,若∠3=40°,则∠4等于
如图,直线a,b被直线c所截,a∥b,∠1=∠2,若∠3=40°,则∠4等于