题目内容
1.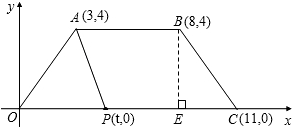 如图,在平面直角坐标系内,梯形OABC的顶点坐标分别是:A(3,4),B(8,4),C(11,0),点P(t,0)是线段OC上一点,设四边形ABCP的面积为S.
如图,在平面直角坐标系内,梯形OABC的顶点坐标分别是:A(3,4),B(8,4),C(11,0),点P(t,0)是线段OC上一点,设四边形ABCP的面积为S.(1)过点B作BE⊥x轴于点E,则BE=4,用含t的代数式表示PC=11-t.
(2)求S与t的函数关系.
(3)当S=20时,直接写出线段AB与CP的长.
分析 (1)过点B作BE⊥X轴于点E,根据B(8,4),即可求得BE=4,由于C(11,0),点P(t,0),于是得到OC=11,OP=t,即可得到结论;
(2)根据梯形面积公式S=$\frac{1}{2}$(AB+PC)BE,代入数据即可得到结论;
(3)把S=20,代入S=-2t+32得,得出t=6,求出PC=11-t=5=AB即可.
解答 解:(1)过点B作BE⊥x轴于点E, 如图所示:
如图所示:
∵B(8,4),
∴BE=4,
∵C(11,0),点P(t,0),
∴OC=11,OP=t,
∴用含t的代数式表示PC=11-t;
故答案为:4,11-t;
(2)根据梯形的面积公式得:S=$\frac{1}{2}$(AB+PC)BE=$\frac{1}{2}$(5+11-t)×4,
∴S与t的函数关系为:S=-2t+32;
(3)当S=20时,-2t+32=20,
解得:t=6.
此时,PC=11-t=5=AB.
点评 本题考查了梯形的面积、坐标与图形性质;熟练掌握梯形的面积,由梯形的面积公式得出S与t的函数关系是解决(2)的关键.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
11.下面四个等式中成立的是( )
| A. | (-a)2=-a2 | B. | -a3=a3 | C. | a2=|a|2 | D. | a3=|a|3 |
6.已知$\frac{x}{y}$=$\frac{1}{3}$,那么$\frac{x+y}{x-y}$的值为( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
10.抛物线y=(x+1)2-1的顶点坐标为( )
| A. | (-1,-1) | B. | (1,-1) | C. | (-1,1) | D. | (1,1) |
11.某个体水果店经营香蕉,每千克进价2.6元,售价3.4元,10月1日至10月5日经营情况如下表:
(1)若9月30日晚库存为0,则10月1日晚库存5kg?
(2)10月1日到10月5日该个体户共赚多少钱?
| 购进kg | 55 | 45 | 50 | 50 | 50 |
| 售出(kg) | 44 | 47.5 | 38 | 44.5 | 51 |
| 损耗(kg) | 6 | 2 | 12 | 5 | 0 |
(2)10月1日到10月5日该个体户共赚多少钱?
 张师傅想用篱笆围一个长方形鸡舍,为了节省篱笆,一边利用房屋外的一面墙(墙的长度为12米),其它三边用篱笆,且中间用篱笆隔开,并在如图位置开两扇门宽各1米的门(门不用篱笆),若鸡舍的宽为(a-3)米,长比宽的$\frac{7}{3}$还多4米.
张师傅想用篱笆围一个长方形鸡舍,为了节省篱笆,一边利用房屋外的一面墙(墙的长度为12米),其它三边用篱笆,且中间用篱笆隔开,并在如图位置开两扇门宽各1米的门(门不用篱笆),若鸡舍的宽为(a-3)米,长比宽的$\frac{7}{3}$还多4米.