题目内容
16.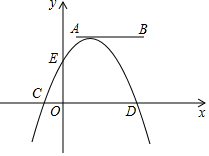 如图,点A,B的坐标分别为(1,4)和(4,4),抛物线y=-(x+m)2+n的顶点M在线段AB上,与x轴交于C、D两点(C在D的左侧),与y轴交于点E.
如图,点A,B的坐标分别为(1,4)和(4,4),抛物线y=-(x+m)2+n的顶点M在线段AB上,与x轴交于C、D两点(C在D的左侧),与y轴交于点E.(1)在点M从点A运动到点B,求点E的纵坐标的变化范围;
(2)当点C和原点O重合时,求此时抛物线解析式,并求出D点坐标.
分析 (1)当M与A重合,当M与B重合,求得抛物线的解析式即可得到结论;
(2)由当M与A重合,抛物线的解析式为y=-(x-1)2+4,得到此时C(-1,0),当点C和原点O重合时,求得抛物线y=-(x-1)2+4向右平移一个单位长度,求得平移后的解析式为y=-(x-1-1)2+4,于是得到结论.
解答 解:(1)当M与A重合,
则M(1,4),
∴抛物线的解析式为y=-(x-1)2+4,
即抛物线的解析式为y=-x2+2x+3
当x=0时,y=3,
当M与B重合,
则M(4,4),
∴抛物线的解析式为y=-(x-4)2+4,
即抛物线的解析式为y=-x2+8x-12
当x=0时,y=-12,
∴在点M从点A运动到点B,点E的纵坐标的变化范围是:3到-12.
(2)∵当M与A重合,抛物线的解析式为y=-(x-1)2+4,
∴抛物线与x轴的交点的坐标为(-1,0),(3,0),
∴此时C(-1,0),
当点C和原点O重合时,
抛物线y=-(x-1)2+4向右平移一个单位长度,
∴平移后的解析式为y=-(x-1-1)2+4,
即y=-(x-2)2+4,
令y=0,则-(x-2)2+4=0,
解得:x1=0,x2=4,
∴D(4,0).
点评 本题主要考查了二次函数的性质,用待定系数法求二次函数的解析式,用直接开平方法解一元二次方程等知识点,理解题意并根据已知求二次函数的解析式是解此题的关键,此题是一个比较典型的题目.

练习册系列答案
相关题目

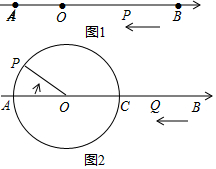 如图1,已知点A,B在以O为原点的数轴上表示的数分别为a,b,且a,b满足|a+4|+(b-10)2=0,动点P从点B出发沿射线BA运动.
如图1,已知点A,B在以O为原点的数轴上表示的数分别为a,b,且a,b满足|a+4|+(b-10)2=0,动点P从点B出发沿射线BA运动.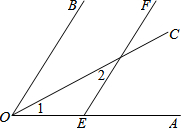 如图,OC是∠AOB的平分线,且∠1=∠2,试说明EF∥OB吗?
如图,OC是∠AOB的平分线,且∠1=∠2,试说明EF∥OB吗?