题目内容
如图3，在直角梯形ABCD中，∠B=∠C=9O°，E、F是BC上两点，若AD=ED，∠ADE=30°，∠FDC=15°，则下列结论：①∠AED=∠DFC;②BE=2CF；③AB- CF=
EF;④S
OAF:SDEF =AF:EF其中正确的结论是( )
EF;④SOAF:SDEF =AF:EF其中正确的结论是( ) | A．①③ | B．②④ | C．①③④ | D．①②④ |
C
①∵∠DFC=∠DAE=75°，
∴AEFD四点共圆，
则所以∠AFB=∠ADE=30°，
所以证明∠AED=∠DFC
故①正确；
②其中用到了AF=2AB，即角AFB=30度，这个条件由四点共圆之后的角AFB=角ADE=30度得到
结论②是错误的，因为AF＞BF，即2AB＞BE+EF，把结论③中EF=2AB-2CF代入得到2CF＞BE，
故②错误；
③作E、F关于直线CD的对称点E’，F’，则可以证明三角形DAF全等于三角形DE’F，所以E’F=2CF+EF=AF=2AB，所以AB-CF=
EF，结论③正确
结论④是正确的，根据三角形DAF全等于三角形DE’F，则可得：S△DAF：S△DEF=AF：EF
故④正确．
故选C
∴AEFD四点共圆，
则所以∠AFB=∠ADE=30°，
所以证明∠AED=∠DFC
故①正确；
②其中用到了AF=2AB，即角AFB=30度，这个条件由四点共圆之后的角AFB=角ADE=30度得到
结论②是错误的，因为AF＞BF，即2AB＞BE+EF，把结论③中EF=2AB-2CF代入得到2CF＞BE，
故②错误；
③作E、F关于直线CD的对称点E’，F’，则可以证明三角形DAF全等于三角形DE’F，所以E’F=2CF+EF=AF=2AB，所以AB-CF=
EF，结论③正确结论④是正确的，根据三角形DAF全等于三角形DE’F，则可得：S△DAF：S△DEF=AF：EF
故④正确．
故选C
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
，
，试说明：
∥
．
的大小（菱形的边长不变），从而改变千斤顶的高度（即A、C之间的距离）.若AB=40cm，当
变为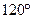
时，千斤顶升高了多少？
中，
，
，高
，则腰
的长为 
