题目内容
10. 二次函数图象的顶点在原点O,经过点A(1,$\frac{1}{4}$);点F(0,1)在y轴上.直线y=-1与y轴交于点H.
二次函数图象的顶点在原点O,经过点A(1,$\frac{1}{4}$);点F(0,1)在y轴上.直线y=-1与y轴交于点H.(1)求二次函数的解析式;
(2)点P是(1)中图象上的点,过点P作x轴的垂线与直线y=-1交于点M,求证:△PFM为等腰三角形;
(3)点P是(1)中图象上的点,过点P作x轴的垂线与直线y=-1交于点M,作PQ⊥FM交FM于点Q,当点P从横坐标2015处运动到横坐标2016处时,请直接写出点Q运动的路径长.
分析 (1)设抛物线的解析式为y=ax2,将点A的坐标代入求得a的值即可;
(2)由两点间的距离公式可求得PM和PF的长,从而得到PM=PF;
(3)由等腰三角形的性质可知点Q是FM的中点,从而得到OQ是△FHM的中位线,由三角形中位线的性质可求得当点P的横坐标为2015时,OQ=1007.5;当点P的横坐标为2016时,OQ=1008,故此可求得点Q运动的路径长.
解答 解:(1)二次函数解析式为:y=ax2,
∵经过点A(1,$\frac{1}{4}$),
∴a=$\frac{1}{4}$,
∴二次函数的解析式y=$\frac{1}{4}$x2.
(2)∵点P是(1)中图象上的点,过点P作x轴的垂线与直线y=-1交于点M,
设P(x,$\frac{1}{4}$x2),则M(x,-1),
∴PM=$\frac{1}{4}$x2+1.
由两点间的距离公式可知:PF=$\sqrt{(x-0)^{2}+(\frac{1}{4}{x}^{2}-1)^{2}}$=$\sqrt{{x}^{2}+\frac{1}{16}{x}^{2}-\frac{1}{2}{x}^{2}+1}$=$\sqrt{\frac{1}{16}{x}^{2}+\frac{1}{2}{x}^{2}+1}$=$\frac{1}{4}{x}^{2}+1$.
∴PF=PM 即△PFM为等腰三角形.
(3)如图所示:过点P作PQ⊥FM,垂足为Q.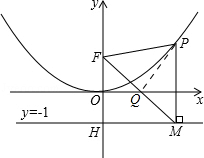
∵PF=PM,PQ⊥FM,
∴FQ=QM.
∵OF=OH,FQ=QM,
∴OQ∥HM,且OQ=$\frac{1}{2}$MH.
当点P的横坐标为2015时,OQ=$\frac{1}{2}$HM=$\frac{1}{2}×2015$=1007.5.
当点P的横坐标为2016时,OQ=$\frac{1}{2}$HM=$\frac{1}{2}×2016$=1008.
∴点Q运动的路径长=1008-1007.5=0.5.
点评 本题主要考查的是二次函数的综合应用、等腰三角形的性质、三角形中位线的性质,证得OQ是△FHM的中位线,利用三角形的中位线的性质求得当点P的横坐标为2015时和当点P的横坐标为2016时OQ的长是解题的关键.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案| A. | 2014 | B. | 2 | C. | $\frac{1}{2}$ | D. | -1 |
| A. | a | B. | b+a | C. | b-a | D. | 不能确定 |
| A. | $\frac{1}{3}$x=0变形得x=3 | B. | 3x=2x-2变形得3x-2x=2 | ||
| C. | 3x=2变形得x=$\frac{3}{2}$ | D. | $\frac{2}{3}x-1=x$变形得2x-3=3x |
 2003~2005年某市的财政收入情况如图所示.根据图中的信息,解答下列问题:
2003~2005年某市的财政收入情况如图所示.根据图中的信息,解答下列问题: PA为⊙O切线,A为切点,PO交⊙O于点B,OA=3,OP=6,则∠BAP度数为30度.
PA为⊙O切线,A为切点,PO交⊙O于点B,OA=3,OP=6,则∠BAP度数为30度.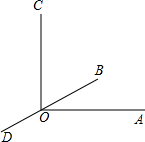 如图,已知∠AOC=90°,直线BD过点O,∠COD=115°15′,则∠AOB=25°15′.
如图,已知∠AOC=90°,直线BD过点O,∠COD=115°15′,则∠AOB=25°15′.