��Ŀ����
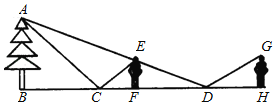
����Ŀ����ͼ������������Ա������O���׳�һ������������1m���ĵ�A�ɳ�������е����߶���4m����ߴ�����ɳ����ˮƽ������6m���ҷ��е�·����������һ���֣��Ե�OΪ����ԭ�㣬��ֱ���ϵķ���Ϊy�������������е�ˮƽ����Ϊx���������������ϵ��������һ���㣮���ο����ݣ�4![]() ��7��
��7��

��1��������ķ��и߶�y��m�������ˮƽ����x��m��֮��ĺ�����ϵʽ��
��2����û�ж�Ա���ŵ�����£�����е���Զˮƽ�����Ƕ��٣�����ȷ����λ��
��3�����Է�һ��1.7m�Ķ�Ա�ھ����C 3m�ĵ�H����Ծ��0.3m�������أ���������Ա����������
���𰸡���1��y=��![]() ��x��6��2+4����2������е���Զˮƽ������13�ף���3��������Ա�������������ɼ�����
��x��6��2+4����2������е���Զˮƽ������13�ף���3��������Ա�������������ɼ�����
��������
��1���躯��Ϊ����ʽ���ٰѣ�0��1�����뼴����⣻
��2����y=0�������x��
��3����x=13��3=10���������ʽ���y���ٸ�1.7+0.3���бȽϼ����ж�.
��1����h=4ʱ��y=a��x��6��2+4����A��0��1��
��1=a��0��6��2+4��
��a=��![]() ��
��
��y=��![]() ��x��6��2+4��
��x��6��2+4��
��2����y=0����0=��![]() ��x��6��2+4����ã�x1=4
��x��6��2+4����ã�x1=4![]() +6��13��x2=��4
+6��13��x2=��4![]() +6��0����ȥ��
+6��0����ȥ��
������е���Զˮƽ������13�ף�
��3����x=13��3=10ʱ��y=��![]() ��10��6��2+4=
��10��6��2+4=![]() ��1.7+0.3=2��
��1.7+0.3=2��
��������Ա����������.

 ��ʱѵ���������������ϵ�д�
��ʱѵ���������������ϵ�д� �ƸԾ���Ȥζ����ϵ�д�
�ƸԾ���Ȥζ����ϵ�д� ����С����ҵ��ϵ�д�
����С����ҵ��ϵ�д�